`sklearn.gaussian_process.kernels`.DotProduct¶

class sklearn.gaussian_process.kernels.DotProduct(sigma_0=1.0, sigma_0_bounds=(1e-05, 100000.0))[source]¶

Dot-Product kernel.

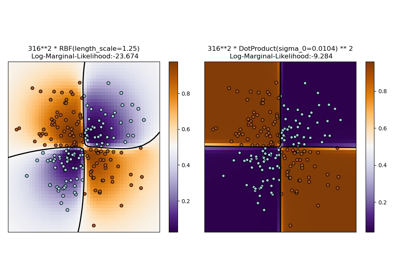
The DotProduct kernel is non-stationary and can be obtained from linear regression by putting \(N(0, 1)\) priors on the coefficients of \(x_d (d = 1, . . . , D)\) and a prior of \(N(0, \sigma_0^2)\) on the bias. The DotProduct kernel is invariant to a rotation of the coordinates about the origin, but not translations. It is parameterized by a parameter sigma_0 \(\sigma\) which controls the inhomogenity of the kernel. For \(\sigma_0^2 =0\), the kernel is called the homogeneous linear kernel, otherwise it is inhomogeneous. The kernel is given by

\[k(x_i, x_j) = \sigma_0 ^ 2 + x_i \cdot x_j\]

The DotProduct kernel is commonly combined with exponentiation.

See [1], Chapter 4, Section 4.2, for further details regarding the DotProduct kernel.

Read more in the User Guide.

New in version 0.18.

Parameters

sigma_0float >= 0, default=1.0: Parameter controlling the inhomogenity of the kernel. If sigma_0=0, the kernel is homogeneous.
sigma_0_boundspair of floats >= 0 or “fixed”, default=(1e-5, 1e5): The lower and upper bound on ‘sigma_0’. If set to “fixed”, ‘sigma_0’ cannot be changed during hyperparameter tuning.

Attributes

bounds: Returns the log-transformed bounds on the theta.
hyperparameter_sigma_0
hyperparameters: Returns a list of all hyperparameter specifications.
n_dims: Returns the number of non-fixed hyperparameters of the kernel.
requires_vector_input: Returns whether the kernel is defined on fixed-length feature vectors or generic objects.
theta: Returns the (flattened, log-transformed) non-fixed hyperparameters.

References

1: Carl Edward Rasmussen, Christopher K. I. Williams (2006). “Gaussian Processes for Machine Learning”. The MIT Press.

Examples

>>> from sklearn.datasets import make_friedman2
>>> from sklearn.gaussian_process import GaussianProcessRegressor
>>> from sklearn.gaussian_process.kernels import DotProduct, WhiteKernel
>>> X, y = make_friedman2(n_samples=500, noise=0, random_state=0)
>>> kernel = DotProduct() + WhiteKernel()
>>> gpr = GaussianProcessRegressor(kernel=kernel,
...         random_state=0).fit(X, y)
>>> gpr.score(X, y)
0.3680...
>>> gpr.predict(X[:2,:], return_std=True)
(array([653.0..., 592.1...]), array([316.6..., 316.6...]))

Methods

`__call__`(X[, Y, eval_gradient])	Return the kernel k(X, Y) and optionally its gradient.
`clone_with_theta`(theta)	Returns a clone of self with given hyperparameters theta.
`diag`(X)	Returns the diagonal of the kernel k(X, X).
`get_params`([deep])	Get parameters of this kernel.
`is_stationary`()	Returns whether the kernel is stationary.
`set_params`(**params)	Set the parameters of this kernel.

__call__(X, Y=None, eval_gradient=False)[source]¶

Return the kernel k(X, Y) and optionally its gradient.

Parameters

Xndarray of shape (n_samples_X, n_features): Left argument of the returned kernel k(X, Y)
Yndarray of shape (n_samples_Y, n_features), default=None: Right argument of the returned kernel k(X, Y). If None, k(X, X) if evaluated instead.
eval_gradientbool, default=False: Determines whether the gradient with respect to the log of the kernel hyperparameter is computed. Only supported when Y is None.

Returns

Kndarray of shape (n_samples_X, n_samples_Y): Kernel k(X, Y)
K_gradientndarray of shape (n_samples_X, n_samples_X, n_dims), optional: The gradient of the kernel k(X, X) with respect to the log of the hyperparameter of the kernel. Only returned when eval_gradient is True.

property bounds¶

Returns the log-transformed bounds on the theta.

Returns

boundsndarray of shape (n_dims, 2): The log-transformed bounds on the kernel’s hyperparameters theta

clone_with_theta(theta)[source]¶

Returns a clone of self with given hyperparameters theta.

Parameters

thetandarray of shape (n_dims,): The hyperparameters

diag(X)[source]¶

Returns the diagonal of the kernel k(X, X).

The result of this method is identical to np.diag(self(X)); however, it can be evaluated more efficiently since only the diagonal is evaluated.

Parameters

Xndarray of shape (n_samples_X, n_features): Left argument of the returned kernel k(X, Y).

Returns

K_diagndarray of shape (n_samples_X,): Diagonal of kernel k(X, X).

get_params(deep=True)[source]¶

Get parameters of this kernel.

Parameters

deepbool, default=True: If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns

paramsdict: Parameter names mapped to their values.

property hyperparameters¶: Returns a list of all hyperparameter specifications.

is_stationary()[source]¶: Returns whether the kernel is stationary.

property n_dims¶: Returns the number of non-fixed hyperparameters of the kernel.

property requires_vector_input¶: Returns whether the kernel is defined on fixed-length feature vectors or generic objects. Defaults to True for backward compatibility.

set_params(**params)[source]¶

Set the parameters of this kernel.

The method works on simple kernels as well as on nested kernels. The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Returns

self

property theta¶

Returns the (flattened, log-transformed) non-fixed hyperparameters.

Note that theta are typically the log-transformed values of the kernel’s hyperparameters as this representation of the search space is more amenable for hyperparameter search, as hyperparameters like length-scales naturally live on a log-scale.

Returns

thetandarray of shape (n_dims,): The non-fixed, log-transformed hyperparameters of the kernel

Examples using `sklearn.gaussian_process.kernels.DotProduct`¶

sklearn.gaussian_process.kernels.DotProduct¶

Examples using sklearn.gaussian_process.kernels.DotProduct¶

`sklearn.gaussian_process.kernels`.DotProduct¶

Examples using `sklearn.gaussian_process.kernels.DotProduct`¶