Note

Click here to download the full example code or to run this example in your browser via Binder

Combine predictors using stacking¶

Stacking refers to a method to blend estimators. In this strategy, some estimators are individually fitted on some training data while a final estimator is trained using the stacked predictions of these base estimators.

In this example, we illustrate the use case in which different regressors are stacked together and a final linear penalized regressor is used to output the prediction. We compare the performance of each individual regressor with the stacking strategy. Stacking slightly improves the overall performance.

# Authors: Guillaume Lemaitre <g.lemaitre58@gmail.com>
#          Maria Telenczuk    <https://github.com/maikia>
# License: BSD 3 clause

from sklearn import set_config

set_config(display="diagram")

Download the dataset¶

We will use Ames Housing dataset which was first compiled by Dean De Cock and became better known after it was used in Kaggle challenge. It is a set of 1460 residential homes in Ames, Iowa, each described by 80 features. We will use it to predict the final logarithmic price of the houses. In this example we will use only 20 most interesting features chosen using GradientBoostingRegressor() and limit number of entries (here we won’t go into the details on how to select the most interesting features).

The Ames housing dataset is not shipped with scikit-learn and therefore we will fetch it from OpenML.

import numpy as np

from sklearn.datasets import fetch_openml
from sklearn.utils import shuffle


def load_ames_housing():
    df = fetch_openml(name="house_prices", as_frame=True)
    X = df.data
    y = df.target

    features = [
        "YrSold",
        "HeatingQC",
        "Street",
        "YearRemodAdd",
        "Heating",
        "MasVnrType",
        "BsmtUnfSF",
        "Foundation",
        "MasVnrArea",
        "MSSubClass",
        "ExterQual",
        "Condition2",
        "GarageCars",
        "GarageType",
        "OverallQual",
        "TotalBsmtSF",
        "BsmtFinSF1",
        "HouseStyle",
        "MiscFeature",
        "MoSold",
    ]

    X = X[features]
    X, y = shuffle(X, y, random_state=0)

    X = X[:600]
    y = y[:600]
    return X, np.log(y)


X, y = load_ames_housing()

Measure and plot the results¶

Now we can use Ames Housing dataset to make the predictions. We check the performance of each individual predictor as well as of the stack of the regressors.

The function plot_regression_results is used to plot the predicted and true targets.

import time
import matplotlib.pyplot as plt
from sklearn.model_selection import cross_validate, cross_val_predict


def plot_regression_results(ax, y_true, y_pred, title, scores, elapsed_time):
    """Scatter plot of the predicted vs true targets."""
    ax.plot(
        [y_true.min(), y_true.max()], [y_true.min(), y_true.max()], "--r", linewidth=2
    )
    ax.scatter(y_true, y_pred, alpha=0.2)

    ax.spines["top"].set_visible(False)
    ax.spines["right"].set_visible(False)
    ax.get_xaxis().tick_bottom()
    ax.get_yaxis().tick_left()
    ax.spines["left"].set_position(("outward", 10))
    ax.spines["bottom"].set_position(("outward", 10))
    ax.set_xlim([y_true.min(), y_true.max()])
    ax.set_ylim([y_true.min(), y_true.max()])
    ax.set_xlabel("Measured")
    ax.set_ylabel("Predicted")
    extra = plt.Rectangle(
        (0, 0), 0, 0, fc="w", fill=False, edgecolor="none", linewidth=0
    )
    ax.legend([extra], [scores], loc="upper left")
    title = title + "\n Evaluation in {:.2f} seconds".format(elapsed_time)
    ax.set_title(title)


fig, axs = plt.subplots(2, 2, figsize=(9, 7))
axs = np.ravel(axs)

for ax, (name, est) in zip(
    axs, estimators + [("Stacking Regressor", stacking_regressor)]
):
    start_time = time.time()
    score = cross_validate(
        est, X, y, scoring=["r2", "neg_mean_absolute_error"], n_jobs=2, verbose=0
    )
    elapsed_time = time.time() - start_time

    y_pred = cross_val_predict(est, X, y, n_jobs=2, verbose=0)

    plot_regression_results(
        ax,
        y,
        y_pred,
        name,
        (r"$R^2={:.2f} \pm {:.2f}$" + "\n" + r"$MAE={:.2f} \pm {:.2f}$").format(
            np.mean(score["test_r2"]),
            np.std(score["test_r2"]),
            -np.mean(score["test_neg_mean_absolute_error"]),
            np.std(score["test_neg_mean_absolute_error"]),
        ),
        elapsed_time,
    )

plt.suptitle("Single predictors versus stacked predictors")
plt.tight_layout()
plt.subplots_adjust(top=0.9)
plt.show()

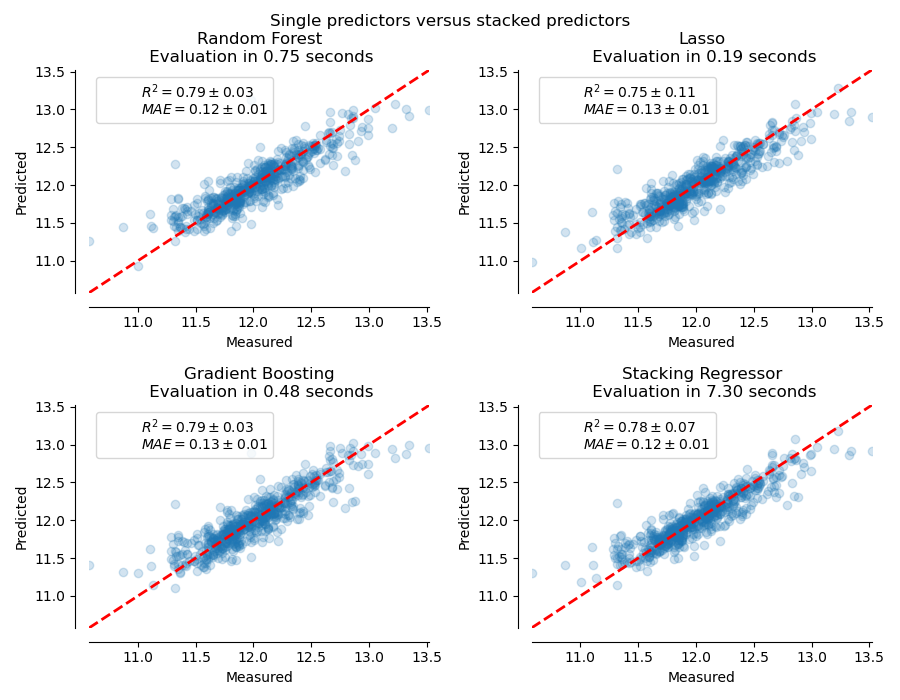
Single predictors versus stacked predictors, Random Forest Evaluation in 0.75 seconds, Lasso Evaluation in 0.19 seconds, Gradient Boosting Evaluation in 0.48 seconds, Stacking Regressor Evaluation in 7.30 seconds

The stacked regressor will combine the strengths of the different regressors. However, we also see that training the stacked regressor is much more computationally expensive.

Total running time of the script: ( 0 minutes 18.008 seconds)

Gallery generated by Sphinx-Gallery

Combine predictors using stacking¶

Download the dataset¶

Make pipeline to preprocess the data¶

Stack of predictors on a single data set¶

Measure and plot the results¶