sklearn.preprocessing.PolynomialFeatures¶
-
class
sklearn.preprocessing.PolynomialFeatures(degree=2, *, interaction_only=False, include_bias=True, order='C')[source]¶ Generate polynomial and interaction features.
Generate a new feature matrix consisting of all polynomial combinations of the features with degree less than or equal to the specified degree. For example, if an input sample is two dimensional and of the form [a, b], the degree-2 polynomial features are [1, a, b, a^2, ab, b^2].
- Parameters
- degreeinteger
The degree of the polynomial features. Default = 2.
- interaction_onlyboolean, default = False
If true, only interaction features are produced: features that are products of at most
degreedistinct input features (so notx[1] ** 2,x[0] * x[2] ** 3, etc.).- include_biasboolean
If True (default), then include a bias column, the feature in which all polynomial powers are zero (i.e. a column of ones - acts as an intercept term in a linear model).
- orderstr in {‘C’, ‘F’}, default ‘C’
Order of output array in the dense case. ‘F’ order is faster to compute, but may slow down subsequent estimators.
New in version 0.21.
- Attributes
- powers_array, shape (n_output_features, n_input_features)
powers_[i, j] is the exponent of the jth input in the ith output.
- n_input_features_int
The total number of input features.
- n_output_features_int
The total number of polynomial output features. The number of output features is computed by iterating over all suitably sized combinations of input features.
Notes
Be aware that the number of features in the output array scales polynomially in the number of features of the input array, and exponentially in the degree. High degrees can cause overfitting.
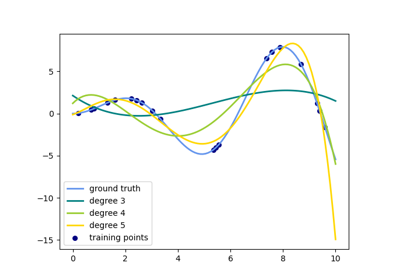
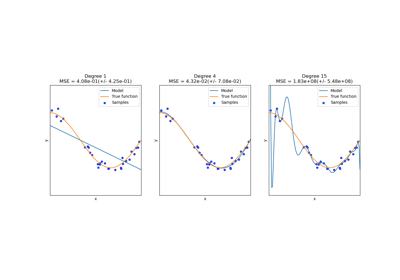
See examples/linear_model/plot_polynomial_interpolation.py
Examples
>>> import numpy as np >>> from sklearn.preprocessing import PolynomialFeatures >>> X = np.arange(6).reshape(3, 2) >>> X array([[0, 1], [2, 3], [4, 5]]) >>> poly = PolynomialFeatures(2) >>> poly.fit_transform(X) array([[ 1., 0., 1., 0., 0., 1.], [ 1., 2., 3., 4., 6., 9.], [ 1., 4., 5., 16., 20., 25.]]) >>> poly = PolynomialFeatures(interaction_only=True) >>> poly.fit_transform(X) array([[ 1., 0., 1., 0.], [ 1., 2., 3., 6.], [ 1., 4., 5., 20.]])
Methods
fit(X[, y])Compute number of output features.
fit_transform(X[, y])Fit to data, then transform it.
get_feature_names([input_features])Return feature names for output features
get_params([deep])Get parameters for this estimator.
set_params(**params)Set the parameters of this estimator.
transform(X)Transform data to polynomial features
-
__init__(degree=2, *, interaction_only=False, include_bias=True, order='C')[source]¶ Initialize self. See help(type(self)) for accurate signature.
-
fit(X, y=None)[source]¶ Compute number of output features.
- Parameters
- Xarray-like, shape (n_samples, n_features)
The data.
- Returns
- selfinstance
-
fit_transform(X, y=None, **fit_params)[source]¶ Fit to data, then transform it.
Fits transformer to X and y with optional parameters fit_params and returns a transformed version of X.
- Parameters
- X{array-like, sparse matrix, dataframe} of shape (n_samples, n_features)
- yndarray of shape (n_samples,), default=None
Target values.
- **fit_paramsdict
Additional fit parameters.
- Returns
- X_newndarray array of shape (n_samples, n_features_new)
Transformed array.
-
get_feature_names(input_features=None)[source]¶ Return feature names for output features
- Parameters
- input_featureslist of string, length n_features, optional
String names for input features if available. By default, “x0”, “x1”, … “xn_features” is used.
- Returns
- output_feature_nameslist of string, length n_output_features
-
get_params(deep=True)[source]¶ Get parameters for this estimator.
- Parameters
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns
- paramsmapping of string to any
Parameter names mapped to their values.
-
set_params(**params)[source]¶ Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as pipelines). The latter have parameters of the form
<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters
- **paramsdict
Estimator parameters.
- Returns
- selfobject
Estimator instance.
-
transform(X)[source]¶ Transform data to polynomial features
- Parameters
- Xarray-like or CSR/CSC sparse matrix, shape [n_samples, n_features]
The data to transform, row by row.
Prefer CSR over CSC for sparse input (for speed), but CSC is required if the degree is 4 or higher. If the degree is less than 4 and the input format is CSC, it will be converted to CSR, have its polynomial features generated, then converted back to CSC.
If the degree is 2 or 3, the method described in “Leveraging Sparsity to Speed Up Polynomial Feature Expansions of CSR Matrices Using K-Simplex Numbers” by Andrew Nystrom and John Hughes is used, which is much faster than the method used on CSC input. For this reason, a CSC input will be converted to CSR, and the output will be converted back to CSC prior to being returned, hence the preference of CSR.
- Returns
- XPnp.ndarray or CSR/CSC sparse matrix, shape [n_samples, NP]
The matrix of features, where NP is the number of polynomial features generated from the combination of inputs.