Note
Click here to download the full example code or to run this example in your browser via Binder
Effect of transforming the targets in regression model¶
In this example, we give an overview of the
sklearn.compose.TransformedTargetRegressor. Two examples
illustrate the benefit of transforming the targets before learning a linear
regression model. The first example uses synthetic data while the second
example is based on the Boston housing data set.
# Author: Guillaume Lemaitre <guillaume.lemaitre@inria.fr>
# License: BSD 3 clause
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
print(__doc__)
Synthetic example¶
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import RidgeCV
from sklearn.compose import TransformedTargetRegressor
from sklearn.metrics import median_absolute_error, r2_score
from sklearn.utils.fixes import parse_version
# `normed` is being deprecated in favor of `density` in histograms
if parse_version(matplotlib.__version__) >= parse_version('2.1'):
density_param = {'density': True}
else:
density_param = {'normed': True}
A synthetic random regression problem is generated. The targets y are
modified by: (i) translating all targets such that all entries are
non-negative and (ii) applying an exponential function to obtain non-linear
targets which cannot be fitted using a simple linear model.
Therefore, a logarithmic (np.log1p) and an exponential function
(np.expm1) will be used to transform the targets before training a linear
regression model and using it for prediction.
X, y = make_regression(n_samples=10000, noise=100, random_state=0)
y = np.exp((y + abs(y.min())) / 200)
y_trans = np.log1p(y)
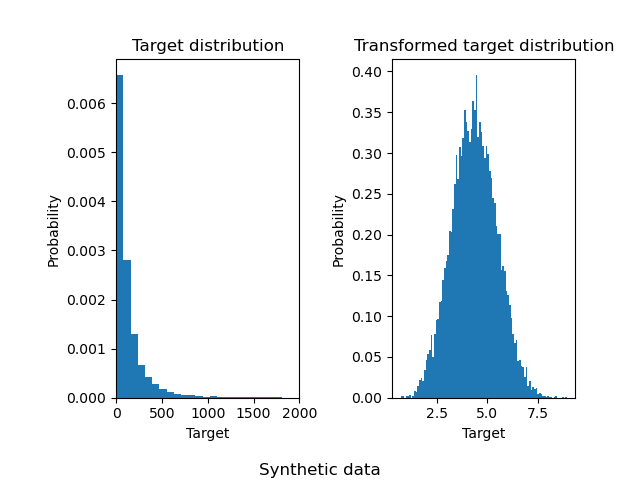
The following illustrate the probability density functions of the target before and after applying the logarithmic functions.
f, (ax0, ax1) = plt.subplots(1, 2)
ax0.hist(y, bins=100, **density_param)
ax0.set_xlim([0, 2000])
ax0.set_ylabel('Probability')
ax0.set_xlabel('Target')
ax0.set_title('Target distribution')
ax1.hist(y_trans, bins=100, **density_param)
ax1.set_ylabel('Probability')
ax1.set_xlabel('Target')
ax1.set_title('Transformed target distribution')
f.suptitle("Synthetic data", y=0.035)
f.tight_layout(rect=[0.05, 0.05, 0.95, 0.95])
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
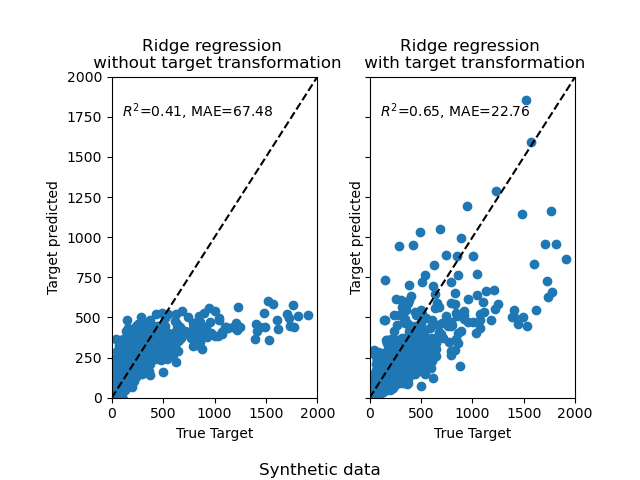
At first, a linear model will be applied on the original targets. Due to the non-linearity, the model trained will not be precise during the prediction. Subsequently, a logarithmic function is used to linearize the targets, allowing better prediction even with a similar linear model as reported by the median absolute error (MAE).
f, (ax0, ax1) = plt.subplots(1, 2, sharey=True)
regr = RidgeCV()
regr.fit(X_train, y_train)
y_pred = regr.predict(X_test)
ax0.scatter(y_test, y_pred)
ax0.plot([0, 2000], [0, 2000], '--k')
ax0.set_ylabel('Target predicted')
ax0.set_xlabel('True Target')
ax0.set_title('Ridge regression \n without target transformation')
ax0.text(100, 1750, r'$R^2$=%.2f, MAE=%.2f' % (
r2_score(y_test, y_pred), median_absolute_error(y_test, y_pred)))
ax0.set_xlim([0, 2000])
ax0.set_ylim([0, 2000])
regr_trans = TransformedTargetRegressor(regressor=RidgeCV(),
func=np.log1p,
inverse_func=np.expm1)
regr_trans.fit(X_train, y_train)
y_pred = regr_trans.predict(X_test)
ax1.scatter(y_test, y_pred)
ax1.plot([0, 2000], [0, 2000], '--k')
ax1.set_ylabel('Target predicted')
ax1.set_xlabel('True Target')
ax1.set_title('Ridge regression \n with target transformation')
ax1.text(100, 1750, r'$R^2$=%.2f, MAE=%.2f' % (
r2_score(y_test, y_pred), median_absolute_error(y_test, y_pred)))
ax1.set_xlim([0, 2000])
ax1.set_ylim([0, 2000])
f.suptitle("Synthetic data", y=0.035)
f.tight_layout(rect=[0.05, 0.05, 0.95, 0.95])
Real-world data set¶
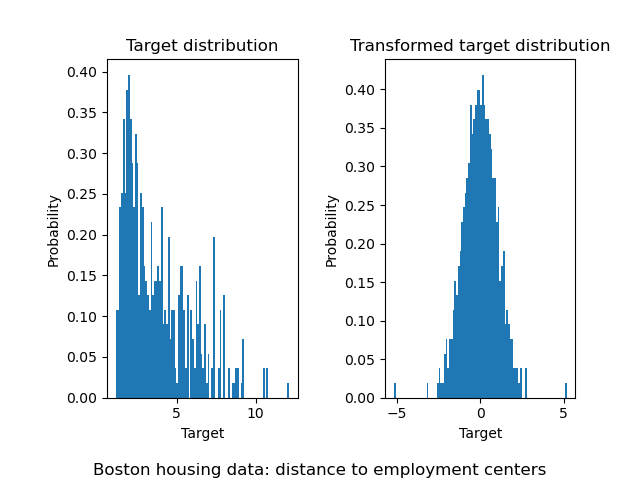
In a similar manner, the boston housing data set is used to show the impact of transforming the targets before learning a model. In this example, the targets to be predicted corresponds to the weighted distances to the five Boston employment centers.
from sklearn.datasets import load_boston
from sklearn.preprocessing import QuantileTransformer, quantile_transform
dataset = load_boston()
target = np.array(dataset.feature_names) == "DIS"
X = dataset.data[:, np.logical_not(target)]
y = dataset.data[:, target].squeeze()
y_trans = quantile_transform(dataset.data[:, target],
n_quantiles=300,
output_distribution='normal',
copy=True).squeeze()
A sklearn.preprocessing.QuantileTransformer is used such that the
targets follows a normal distribution before applying a
sklearn.linear_model.RidgeCV model.
f, (ax0, ax1) = plt.subplots(1, 2)
ax0.hist(y, bins=100, **density_param)
ax0.set_ylabel('Probability')
ax0.set_xlabel('Target')
ax0.set_title('Target distribution')
ax1.hist(y_trans, bins=100, **density_param)
ax1.set_ylabel('Probability')
ax1.set_xlabel('Target')
ax1.set_title('Transformed target distribution')
f.suptitle("Boston housing data: distance to employment centers", y=0.035)
f.tight_layout(rect=[0.05, 0.05, 0.95, 0.95])
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
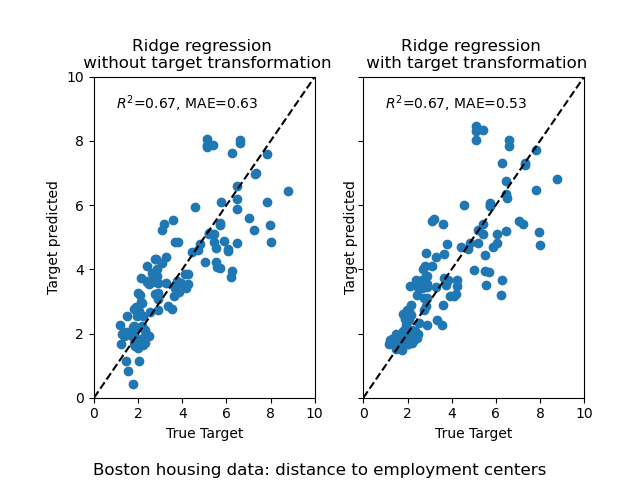
The effect of the transformer is weaker than on the synthetic data. However, the transform induces a decrease of the MAE.
f, (ax0, ax1) = plt.subplots(1, 2, sharey=True)
regr = RidgeCV()
regr.fit(X_train, y_train)
y_pred = regr.predict(X_test)
ax0.scatter(y_test, y_pred)
ax0.plot([0, 10], [0, 10], '--k')
ax0.set_ylabel('Target predicted')
ax0.set_xlabel('True Target')
ax0.set_title('Ridge regression \n without target transformation')
ax0.text(1, 9, r'$R^2$=%.2f, MAE=%.2f' % (
r2_score(y_test, y_pred), median_absolute_error(y_test, y_pred)))
ax0.set_xlim([0, 10])
ax0.set_ylim([0, 10])
regr_trans = TransformedTargetRegressor(
regressor=RidgeCV(),
transformer=QuantileTransformer(n_quantiles=300,
output_distribution='normal'))
regr_trans.fit(X_train, y_train)
y_pred = regr_trans.predict(X_test)
ax1.scatter(y_test, y_pred)
ax1.plot([0, 10], [0, 10], '--k')
ax1.set_ylabel('Target predicted')
ax1.set_xlabel('True Target')
ax1.set_title('Ridge regression \n with target transformation')
ax1.text(1, 9, r'$R^2$=%.2f, MAE=%.2f' % (
r2_score(y_test, y_pred), median_absolute_error(y_test, y_pred)))
ax1.set_xlim([0, 10])
ax1.set_ylim([0, 10])
f.suptitle("Boston housing data: distance to employment centers", y=0.035)
f.tight_layout(rect=[0.05, 0.05, 0.95, 0.95])
plt.show()
Total running time of the script: ( 0 minutes 1.161 seconds)
