sklearn.preprocessing.StandardScaler

class sklearn.preprocessing.StandardScaler(copy=True, with_mean=True, with_std=True)[source]

Standardize features by removing the mean and scaling to unit variance

The standard score of a sample x is calculated as:

z = (x - u) / s

where u is the mean of the training samples or zero if with_mean=False, and s is the standard deviation of the training samples or one if with_std=False.

Centering and scaling happen independently on each feature by computing the relevant statistics on the samples in the training set. Mean and standard deviation are then stored to be used on later data using the transform method.

Standardization of a dataset is a common requirement for many machine learning estimators: they might behave badly if the individual features do not more or less look like standard normally distributed data (e.g. Gaussian with 0 mean and unit variance).

For instance many elements used in the objective function of a learning algorithm (such as the RBF kernel of Support Vector Machines or the L1 and L2 regularizers of linear models) assume that all features are centered around 0 and have variance in the same order. If a feature has a variance that is orders of magnitude larger that others, it might dominate the objective function and make the estimator unable to learn from other features correctly as expected.

This scaler can also be applied to sparse CSR or CSC matrices by passing with_mean=False to avoid breaking the sparsity structure of the data.

Read more in the User Guide.

Parameters:
copy : boolean, optional, default True

If False, try to avoid a copy and do inplace scaling instead. This is not guaranteed to always work inplace; e.g. if the data is not a NumPy array or scipy.sparse CSR matrix, a copy may still be returned.

with_mean : boolean, True by default

If True, center the data before scaling. This does not work (and will raise an exception) when attempted on sparse matrices, because centering them entails building a dense matrix which in common use cases is likely to be too large to fit in memory.

with_std : boolean, True by default

If True, scale the data to unit variance (or equivalently, unit standard deviation).
Attributes:
scale_ : ndarray or None, shape (n_features,)

Per feature relative scaling of the data. This is calculated using np.sqrt(var_). Equal to None when with_std=False.

New in version 0.17: scale_

mean_ : ndarray or None, shape (n_features,)

The mean value for each feature in the training set. Equal to None when with_mean=False.

var_ : ndarray or None, shape (n_features,)

The variance for each feature in the training set. Used to compute scale_. Equal to None when with_std=False.

n_samples_seen_ : int or array, shape (n_features,)

The number of samples processed by the estimator for each feature. If there are not missing samples, the n_samples_seen will be an integer, otherwise it will be an array. Will be reset on new calls to fit, but increments across partial_fit calls.

See also

scale
Equivalent function without the estimator API.
sklearn.decomposition.PCA
Further removes the linear correlation across features with ‘whiten=True’.

Notes

NaNs are treated as missing values: disregarded in fit, and maintained in transform.

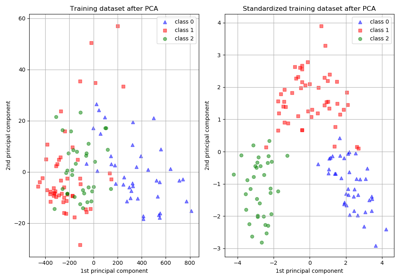
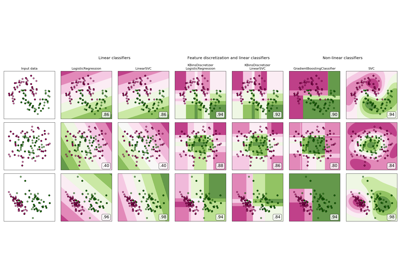
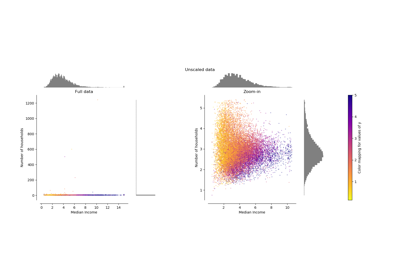
We use a biased estimator for the standard deviation, equivalent to numpy.std(x, ddof=0). Note that the choice of ddof is unlikely to affect model performance.

For a comparison of the different scalers, transformers, and normalizers, see examples/preprocessing/plot_all_scaling.py.

Examples

>>> from sklearn.preprocessing import StandardScaler
>>> data = [[0, 0], [0, 0], [1, 1], [1, 1]]
>>> scaler = StandardScaler()
>>> print(scaler.fit(data))
StandardScaler(copy=True, with_mean=True, with_std=True)
>>> print(scaler.mean_)
[0.5 0.5]
>>> print(scaler.transform(data))
[[-1. -1.]
 [-1. -1.]
 [ 1.  1.]
 [ 1.  1.]]
>>> print(scaler.transform([[2, 2]]))
[[3. 3.]]

Methods

fit(self, X[, y]) Compute the mean and std to be used for later scaling.
fit_transform(self, X[, y]) Fit to data, then transform it.
get_params(self[, deep]) Get parameters for this estimator.
inverse_transform(self, X[, copy]) Scale back the data to the original representation
partial_fit(self, X[, y]) Online computation of mean and std on X for later scaling.
set_params(self, \*\*params) Set the parameters of this estimator.
transform(self, X[, copy]) Perform standardization by centering and scaling
__init__(self, copy=True, with_mean=True, with_std=True)[source]
fit(self, X, y=None)[source]

Compute the mean and std to be used for later scaling.

Parameters:
X : {array-like, sparse matrix}, shape [n_samples, n_features]

The data used to compute the mean and standard deviation used for later scaling along the features axis.

y

Ignored
fit_transform(self, X, y=None, **fit_params)[source]

Fit to data, then transform it.

Fits transformer to X and y with optional parameters fit_params and returns a transformed version of X.

Parameters:
X : numpy array of shape [n_samples, n_features]

Training set.

y : numpy array of shape [n_samples]

Target values.
Returns:
X_new : numpy array of shape [n_samples, n_features_new]

Transformed array.
get_params(self, deep=True)[source]

Get parameters for this estimator.

Parameters:
deep : boolean, optional

If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
params : mapping of string to any

Parameter names mapped to their values.
inverse_transform(self, X, copy=None)[source]

Scale back the data to the original representation

Parameters:
X : array-like, shape [n_samples, n_features]

The data used to scale along the features axis.

copy : bool, optional (default: None)

Copy the input X or not.
Returns:
X_tr : array-like, shape [n_samples, n_features]

Transformed array.
partial_fit(self, X, y=None)[source]

Online computation of mean and std on X for later scaling. All of X is processed as a single batch. This is intended for cases when fit is not feasible due to very large number of n_samples or because X is read from a continuous stream.

The algorithm for incremental mean and std is given in Equation 1.5a,b in Chan, Tony F., Gene H. Golub, and Randall J. LeVeque. “Algorithms for computing the sample variance: Analysis and recommendations.” The American Statistician 37.3 (1983): 242-247:

Parameters:
X : {array-like, sparse matrix}, shape [n_samples, n_features]

The data used to compute the mean and standard deviation used for later scaling along the features axis.

y

Ignored
set_params(self, **params)[source]

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as pipelines). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Returns:
self
transform(self, X, copy=None)[source]

Perform standardization by centering and scaling

Parameters:
X : array-like, shape [n_samples, n_features]

The data used to scale along the features axis.

copy : bool, optional (default: None)

Copy the input X or not.