1.14. Semi-Supervised¶
Semi-supervised learning is a situation
in which in your training data some of the samples are not labeled. The
semi-supervised estimators in sklearn.semi_supervised are able to
make use of this additional unlabeled data to better capture the shape of
the underlying data distribution and generalize better to new samples.
These algorithms can perform well when we have a very small amount of
labeled points and a large amount of unlabeled points.
Unlabeled entries in y
It is important to assign an identifier to unlabeled points along with the
labeled data when training the model with the fit method. The identifier
that this implementation uses is the integer value \(-1\).
1.14.1. Label Propagation¶
Label propagation denotes a few variations of semi-supervised graph inference algorithms.
- A few features available in this model:
- Can be used for classification and regression tasks
- Kernel methods to project data into alternate dimensional spaces
scikit-learn provides two label propagation models:
LabelPropagation and LabelSpreading. Both work by
constructing a similarity graph over all items in the input dataset.
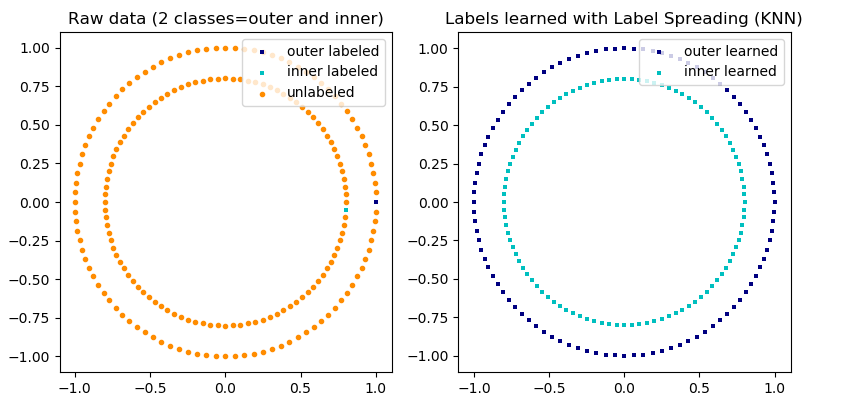
An illustration of label-propagation: the structure of unlabeled observations is consistent with the class structure, and thus the class label can be propagated to the unlabeled observations of the training set.
LabelPropagation and LabelSpreading
differ in modifications to the similarity matrix that graph and the
clamping effect on the label distributions.
Clamping allows the algorithm to change the weight of the true ground labeled
data to some degree. The LabelPropagation algorithm performs hard
clamping of input labels, which means \(\alpha=0\). This clamping factor
can be relaxed, to say \(\alpha=0.2\), which means that we will always
retain 80 percent of our original label distribution, but the algorithm gets to
change its confidence of the distribution within 20 percent.
LabelPropagation uses the raw similarity matrix constructed from
the data with no modifications. In contrast, LabelSpreading
minimizes a loss function that has regularization properties, as such it
is often more robust to noise. The algorithm iterates on a modified
version of the original graph and normalizes the edge weights by
computing the normalized graph Laplacian matrix. This procedure is also
used in Spectral clustering.
Label propagation models have two built-in kernel methods. Choice of kernel effects both scalability and performance of the algorithms. The following are available:
- rbf (\(\exp(-\gamma |x-y|^2), \gamma > 0\)). \(\gamma\) is specified by keyword gamma.
- knn (\(1[x' \in kNN(x)]\)). \(k\) is specified by keyword n_neighbors.
The RBF kernel will produce a fully connected graph which is represented in memory by a dense matrix. This matrix may be very large and combined with the cost of performing a full matrix multiplication calculation for each iteration of the algorithm can lead to prohibitively long running times. On the other hand, the KNN kernel will produce a much more memory-friendly sparse matrix which can drastically reduce running times.
Examples
References
[1] Yoshua Bengio, Olivier Delalleau, Nicolas Le Roux. In Semi-Supervised Learning (2006), pp. 193-216
[2] Olivier Delalleau, Yoshua Bengio, Nicolas Le Roux. Efficient Non-Parametric Function Induction in Semi-Supervised Learning. AISTAT 2005 https://research.microsoft.com/en-us/people/nicolasl/efficient_ssl.pdf

