sklearn.random_projection.johnson_lindenstrauss_min_dim¶
-
sklearn.random_projection.johnson_lindenstrauss_min_dim(n_samples, eps=0.1)[source]¶ Find a ‘safe’ number of components to randomly project to
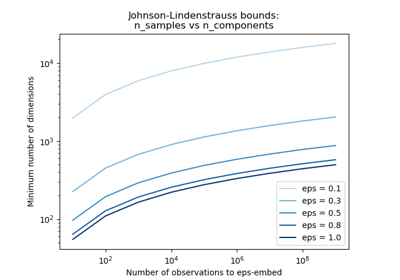
The distortion introduced by a random projection p only changes the distance between two points by a factor (1 +- eps) in an euclidean space with good probability. The projection p is an eps-embedding as defined by:
(1 - eps) ||u - v||^2 < ||p(u) - p(v)||^2 < (1 + eps) ||u - v||^2Where u and v are any rows taken from a dataset of shape [n_samples, n_features], eps is in ]0, 1[ and p is a projection by a random Gaussian N(0, 1) matrix with shape [n_components, n_features] (or a sparse Achlioptas matrix).
The minimum number of components to guarantee the eps-embedding is given by:
n_components >= 4 log(n_samples) / (eps^2 / 2 - eps^3 / 3)Note that the number of dimensions is independent of the original number of features but instead depends on the size of the dataset: the larger the dataset, the higher is the minimal dimensionality of an eps-embedding.
Read more in the User Guide.
Parameters: - n_samples : int or numpy array of int greater than 0,
Number of samples. If an array is given, it will compute a safe number of components array-wise.
- eps : float or numpy array of float in ]0,1[, optional (default=0.1)
Maximum distortion rate as defined by the Johnson-Lindenstrauss lemma. If an array is given, it will compute a safe number of components array-wise.
Returns: - n_components : int or numpy array of int,
The minimal number of components to guarantee with good probability an eps-embedding with n_samples.
References
[1] https://en.wikipedia.org/wiki/Johnson%E2%80%93Lindenstrauss_lemma [2] Sanjoy Dasgupta and Anupam Gupta, 1999, “An elementary proof of the Johnson-Lindenstrauss Lemma.” http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.45.3654 Examples
>>> johnson_lindenstrauss_min_dim(1e6, eps=0.5) 663
>>> johnson_lindenstrauss_min_dim(1e6, eps=[0.5, 0.1, 0.01]) array([ 663, 11841, 1112658])
>>> johnson_lindenstrauss_min_dim([1e4, 1e5, 1e6], eps=0.1) array([ 7894, 9868, 11841])