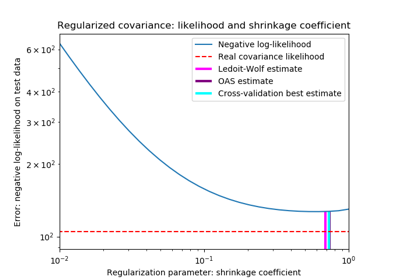
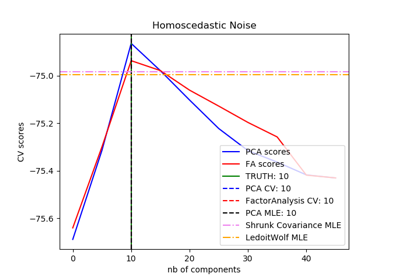
sklearn.covariance.ShrunkCovariance¶
-
class
sklearn.covariance.ShrunkCovariance(store_precision=True, assume_centered=False, shrinkage=0.1)[source]¶ Covariance estimator with shrinkage
Read more in the User Guide.
Parameters: - store_precision : boolean, default True
Specify if the estimated precision is stored
- assume_centered : boolean, default False
If True, data are not centered before computation. Useful when working with data whose mean is almost, but not exactly zero. If False, data are centered before computation.
- shrinkage : float, 0 <= shrinkage <= 1, default 0.1
Coefficient in the convex combination used for the computation of the shrunk estimate.
Attributes: - location_ : array-like, shape (n_features,)
Estimated location, i.e. the estimated mean.
- covariance_ : array-like, shape (n_features, n_features)
Estimated covariance matrix
- precision_ : array-like, shape (n_features, n_features)
Estimated pseudo inverse matrix. (stored only if store_precision is True)
- shrinkage : float, 0 <= shrinkage <= 1
Coefficient in the convex combination used for the computation of the shrunk estimate.
Notes
The regularized covariance is given by:
(1 - shrinkage) * cov + shrinkage * mu * np.identity(n_features)
where mu = trace(cov) / n_features
Examples
>>> import numpy as np >>> from sklearn.covariance import ShrunkCovariance >>> from sklearn.datasets import make_gaussian_quantiles >>> real_cov = np.array([[.8, .3], ... [.3, .4]]) >>> np.random.seed(0) >>> X = np.random.multivariate_normal(mean=[0, 0], ... cov=real_cov, ... size=500) >>> cov = ShrunkCovariance().fit(X) >>> cov.covariance_ array([[0.7387..., 0.2536...], [0.2536..., 0.4110...]]) >>> cov.location_ array([0.0622..., 0.0193...])
Methods
error_norm(comp_cov[, norm, scaling, squared])Computes the Mean Squared Error between two covariance estimators. fit(X[, y])Fits the shrunk covariance model according to the given training data and parameters. get_params([deep])Get parameters for this estimator. get_precision()Getter for the precision matrix. mahalanobis(X)Computes the squared Mahalanobis distances of given observations. score(X_test[, y])Computes the log-likelihood of a Gaussian data set with self.covariance_ as an estimator of its covariance matrix. set_params(**params)Set the parameters of this estimator. -
error_norm(comp_cov, norm='frobenius', scaling=True, squared=True)[source]¶ Computes the Mean Squared Error between two covariance estimators. (In the sense of the Frobenius norm).
Parameters: - comp_cov : array-like, shape = [n_features, n_features]
The covariance to compare with.
- norm : str
The type of norm used to compute the error. Available error types: - ‘frobenius’ (default): sqrt(tr(A^t.A)) - ‘spectral’: sqrt(max(eigenvalues(A^t.A)) where A is the error
(comp_cov - self.covariance_).- scaling : bool
If True (default), the squared error norm is divided by n_features. If False, the squared error norm is not rescaled.
- squared : bool
Whether to compute the squared error norm or the error norm. If True (default), the squared error norm is returned. If False, the error norm is returned.
Returns: - The Mean Squared Error (in the sense of the Frobenius norm) between
- `self` and `comp_cov` covariance estimators.
-
fit(X, y=None)[source]¶ Fits the shrunk covariance model according to the given training data and parameters.
Parameters: - X : array-like, shape = [n_samples, n_features]
Training data, where n_samples is the number of samples and n_features is the number of features.
- y
not used, present for API consistence purpose.
Returns: - self : object
-
get_params(deep=True)[source]¶ Get parameters for this estimator.
Parameters: - deep : boolean, optional
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns: - params : mapping of string to any
Parameter names mapped to their values.
-
get_precision()[source]¶ Getter for the precision matrix.
Returns: - precision_ : array-like
The precision matrix associated to the current covariance object.
-
mahalanobis(X)[source]¶ Computes the squared Mahalanobis distances of given observations.
Parameters: - X : array-like, shape = [n_samples, n_features]
The observations, the Mahalanobis distances of the which we compute. Observations are assumed to be drawn from the same distribution than the data used in fit.
Returns: - dist : array, shape = [n_samples,]
Squared Mahalanobis distances of the observations.
-
score(X_test, y=None)[source]¶ Computes the log-likelihood of a Gaussian data set with self.covariance_ as an estimator of its covariance matrix.
Parameters: - X_test : array-like, shape = [n_samples, n_features]
Test data of which we compute the likelihood, where n_samples is the number of samples and n_features is the number of features. X_test is assumed to be drawn from the same distribution than the data used in fit (including centering).
- y
not used, present for API consistence purpose.
Returns: - res : float
The likelihood of the data set with self.covariance_ as an estimator of its covariance matrix.
-
set_params(**params)[source]¶ Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as pipelines). The latter have parameters of the form
<component>__<parameter>so that it’s possible to update each component of a nested object.Returns: - self