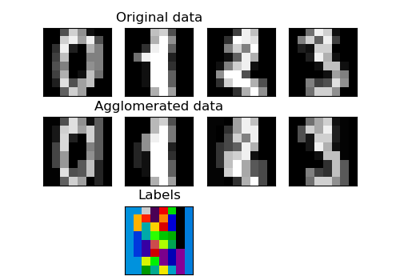
sklearn.cluster.FeatureAgglomeration¶
-
class
sklearn.cluster.FeatureAgglomeration(n_clusters=2, affinity='euclidean', memory=None, connectivity=None, compute_full_tree='auto', linkage='ward', pooling_func=<function mean>)[source]¶ Agglomerate features.
Similar to AgglomerativeClustering, but recursively merges features instead of samples.
Read more in the User Guide.
Parameters: - n_clusters : int, default 2
The number of clusters to find.
- affinity : string or callable, default “euclidean”
Metric used to compute the linkage. Can be “euclidean”, “l1”, “l2”, “manhattan”, “cosine”, or ‘precomputed’. If linkage is “ward”, only “euclidean” is accepted.
- memory : None, str or object with the joblib.Memory interface, optional
Used to cache the output of the computation of the tree. By default, no caching is done. If a string is given, it is the path to the caching directory.
- connectivity : array-like or callable, optional
Connectivity matrix. Defines for each feature the neighboring features following a given structure of the data. This can be a connectivity matrix itself or a callable that transforms the data into a connectivity matrix, such as derived from kneighbors_graph. Default is None, i.e, the hierarchical clustering algorithm is unstructured.
- compute_full_tree : bool or ‘auto’, optional, default “auto”
Stop early the construction of the tree at n_clusters. This is useful to decrease computation time if the number of clusters is not small compared to the number of features. This option is useful only when specifying a connectivity matrix. Note also that when varying the number of clusters and using caching, it may be advantageous to compute the full tree.
- linkage : {“ward”, “complete”, “average”, “single”}, optional (default=”ward”)
Which linkage criterion to use. The linkage criterion determines which distance to use between sets of features. The algorithm will merge the pairs of cluster that minimize this criterion.
- ward minimizes the variance of the clusters being merged.
- average uses the average of the distances of each feature of the two sets.
- complete or maximum linkage uses the maximum distances between all features of the two sets.
- single uses the minimum of the distances between all observations of the two sets.
- pooling_func : callable, default np.mean
This combines the values of agglomerated features into a single value, and should accept an array of shape [M, N] and the keyword argument axis=1, and reduce it to an array of size [M].
Attributes: - labels_ : array-like, (n_features,)
cluster labels for each feature.
- n_leaves_ : int
Number of leaves in the hierarchical tree.
- n_components_ : int
The estimated number of connected components in the graph.
- children_ : array-like, shape (n_nodes-1, 2)
The children of each non-leaf node. Values less than n_features correspond to leaves of the tree which are the original samples. A node i greater than or equal to n_features is a non-leaf node and has children children_[i - n_features]. Alternatively at the i-th iteration, children[i][0] and children[i][1] are merged to form node n_features + i
Examples
>>> import numpy as np >>> from sklearn import datasets, cluster >>> digits = datasets.load_digits() >>> images = digits.images >>> X = np.reshape(images, (len(images), -1)) >>> agglo = cluster.FeatureAgglomeration(n_clusters=32) >>> agglo.fit(X) FeatureAgglomeration(affinity='euclidean', compute_full_tree='auto', connectivity=None, linkage='ward', memory=None, n_clusters=32, pooling_func=...) >>> X_reduced = agglo.transform(X) >>> X_reduced.shape (1797, 32)
Methods
fit(X[, y])Fit the hierarchical clustering on the data fit_transform(X[, y])Fit to data, then transform it. get_params([deep])Get parameters for this estimator. inverse_transform(Xred)Inverse the transformation. pooling_func(a[, axis, dtype, out, keepdims])Compute the arithmetic mean along the specified axis. set_params(**params)Set the parameters of this estimator. transform(X)Transform a new matrix using the built clustering -
__init__(n_clusters=2, affinity='euclidean', memory=None, connectivity=None, compute_full_tree='auto', linkage='ward', pooling_func=<function mean>)[source]¶
-
fit(X, y=None, **params)[source]¶ Fit the hierarchical clustering on the data
Parameters: - X : array-like, shape = [n_samples, n_features]
The data
- y : Ignored
Returns: - self
-
fit_transform(X, y=None, **fit_params)[source]¶ Fit to data, then transform it.
Fits transformer to X and y with optional parameters fit_params and returns a transformed version of X.
Parameters: - X : numpy array of shape [n_samples, n_features]
Training set.
- y : numpy array of shape [n_samples]
Target values.
Returns: - X_new : numpy array of shape [n_samples, n_features_new]
Transformed array.
-
get_params(deep=True)[source]¶ Get parameters for this estimator.
Parameters: - deep : boolean, optional
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns: - params : mapping of string to any
Parameter names mapped to their values.
-
inverse_transform(Xred)[source]¶ Inverse the transformation. Return a vector of size nb_features with the values of Xred assigned to each group of features
Parameters: - Xred : array-like, shape=[n_samples, n_clusters] or [n_clusters,]
The values to be assigned to each cluster of samples
Returns: - X : array, shape=[n_samples, n_features] or [n_features]
A vector of size n_samples with the values of Xred assigned to each of the cluster of samples.
-
pooling_func(a, axis=None, dtype=None, out=None, keepdims=<no value>)[source]¶ Compute the arithmetic mean along the specified axis.
Returns the average of the array elements. The average is taken over the flattened array by default, otherwise over the specified axis. float64 intermediate and return values are used for integer inputs.
Parameters: - a : array_like
Array containing numbers whose mean is desired. If a is not an array, a conversion is attempted.
- axis : None or int or tuple of ints, optional
Axis or axes along which the means are computed. The default is to compute the mean of the flattened array.
New in version 1.7.0.
If this is a tuple of ints, a mean is performed over multiple axes, instead of a single axis or all the axes as before.
- dtype : data-type, optional
Type to use in computing the mean. For integer inputs, the default is float64; for floating point inputs, it is the same as the input dtype.
- out : ndarray, optional
Alternate output array in which to place the result. The default is
None; if provided, it must have the same shape as the expected output, but the type will be cast if necessary. See doc.ufuncs for details.- keepdims : bool, optional
If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the input array.
If the default value is passed, then keepdims will not be passed through to the mean method of sub-classes of ndarray, however any non-default value will be. If the sub-class’ method does not implement keepdims any exceptions will be raised.
Returns: - m : ndarray, see dtype parameter above
If out=None, returns a new array containing the mean values, otherwise a reference to the output array is returned.
See also
average- Weighted average
std,var,nanmean,nanstd,nanvarNotes
The arithmetic mean is the sum of the elements along the axis divided by the number of elements.
Note that for floating-point input, the mean is computed using the same precision the input has. Depending on the input data, this can cause the results to be inaccurate, especially for float32 (see example below). Specifying a higher-precision accumulator using the dtype keyword can alleviate this issue.
By default, float16 results are computed using float32 intermediates for extra precision.
Examples
>>> a = np.array([[1, 2], [3, 4]]) >>> np.mean(a) 2.5 >>> np.mean(a, axis=0) array([ 2., 3.]) >>> np.mean(a, axis=1) array([ 1.5, 3.5])
In single precision, mean can be inaccurate:
>>> a = np.zeros((2, 512*512), dtype=np.float32) >>> a[0, :] = 1.0 >>> a[1, :] = 0.1 >>> np.mean(a) 0.54999924
Computing the mean in float64 is more accurate:
>>> np.mean(a, dtype=np.float64) 0.55000000074505806
-
set_params(**params)[source]¶ Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as pipelines). The latter have parameters of the form
<component>__<parameter>so that it’s possible to update each component of a nested object.Returns: - self
-
transform(X)[source]¶ Transform a new matrix using the built clustering
Parameters: - X : array-like, shape = [n_samples, n_features] or [n_features]
A M by N array of M observations in N dimensions or a length M array of M one-dimensional observations.
Returns: - Y : array, shape = [n_samples, n_clusters] or [n_clusters]
The pooled values for each feature cluster.