Note
Click here to download the full example code
Cross-validation on diabetes Dataset Exercise¶
A tutorial exercise which uses cross-validation with linear models.
This exercise is used in the Cross-validated estimators part of the Model selection: choosing estimators and their parameters section of the A tutorial on statistical-learning for scientific data processing.
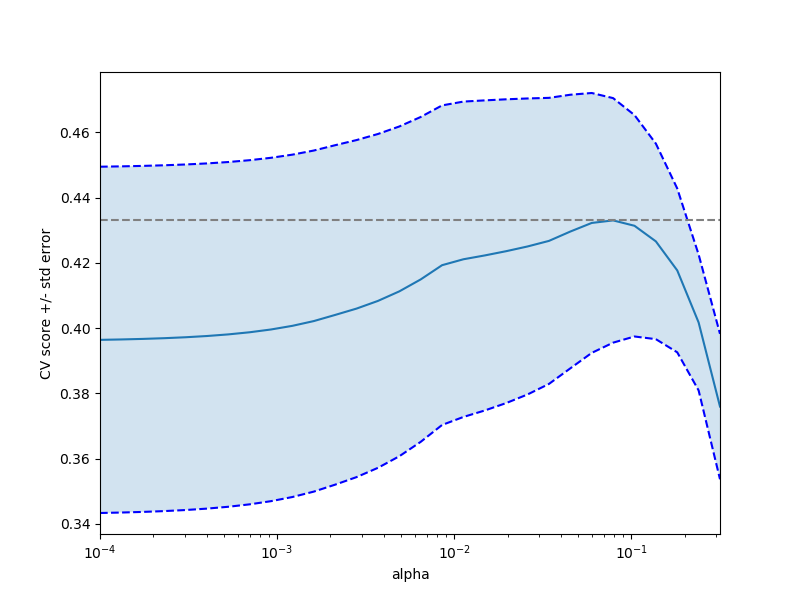
Out:
/home/circleci/project/sklearn/linear_model/coordinate_descent.py:492: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations. Fitting data with very small alpha may cause precision problems.
ConvergenceWarning)
/home/circleci/project/sklearn/linear_model/coordinate_descent.py:492: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations. Fitting data with very small alpha may cause precision problems.
ConvergenceWarning)
Answer to the bonus question: how much can you trust the selection of alpha?
Alpha parameters maximising the generalization score on different
subsets of the data:
[fold 0] alpha: 0.05968, score: 0.54209
[fold 1] alpha: 0.04520, score: 0.15523
[fold 2] alpha: 0.07880, score: 0.45193
Answer: Not very much since we obtained different alphas for different
subsets of the data and moreover, the scores for these alphas differ
quite substantially.
from __future__ import print_function
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.linear_model import LassoCV
from sklearn.linear_model import Lasso
from sklearn.model_selection import KFold
from sklearn.model_selection import GridSearchCV
diabetes = datasets.load_diabetes()
X = diabetes.data[:150]
y = diabetes.target[:150]
lasso = Lasso(random_state=0)
alphas = np.logspace(-4, -0.5, 30)
tuned_parameters = [{'alpha': alphas}]
n_folds = 5
clf = GridSearchCV(lasso, tuned_parameters, cv=n_folds, refit=False)
clf.fit(X, y)
scores = clf.cv_results_['mean_test_score']
scores_std = clf.cv_results_['std_test_score']
plt.figure().set_size_inches(8, 6)
plt.semilogx(alphas, scores)
# plot error lines showing +/- std. errors of the scores
std_error = scores_std / np.sqrt(n_folds)
plt.semilogx(alphas, scores + std_error, 'b--')
plt.semilogx(alphas, scores - std_error, 'b--')
# alpha=0.2 controls the translucency of the fill color
plt.fill_between(alphas, scores + std_error, scores - std_error, alpha=0.2)
plt.ylabel('CV score +/- std error')
plt.xlabel('alpha')
plt.axhline(np.max(scores), linestyle='--', color='.5')
plt.xlim([alphas[0], alphas[-1]])
# #############################################################################
# Bonus: how much can you trust the selection of alpha?
# To answer this question we use the LassoCV object that sets its alpha
# parameter automatically from the data by internal cross-validation (i.e. it
# performs cross-validation on the training data it receives).
# We use external cross-validation to see how much the automatically obtained
# alphas differ across different cross-validation folds.
lasso_cv = LassoCV(alphas=alphas, cv=5, random_state=0)
k_fold = KFold(3)
print("Answer to the bonus question:",
"how much can you trust the selection of alpha?")
print()
print("Alpha parameters maximising the generalization score on different")
print("subsets of the data:")
for k, (train, test) in enumerate(k_fold.split(X, y)):
lasso_cv.fit(X[train], y[train])
print("[fold {0}] alpha: {1:.5f}, score: {2:.5f}".
format(k, lasso_cv.alpha_, lasso_cv.score(X[test], y[test])))
print()
print("Answer: Not very much since we obtained different alphas for different")
print("subsets of the data and moreover, the scores for these alphas differ")
print("quite substantially.")
plt.show()
Total running time of the script: ( 0 minutes 0.536 seconds)

