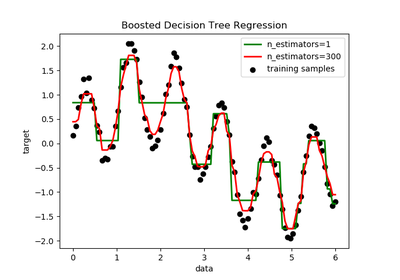
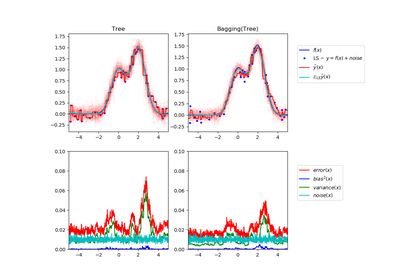
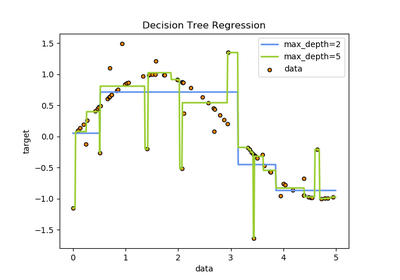
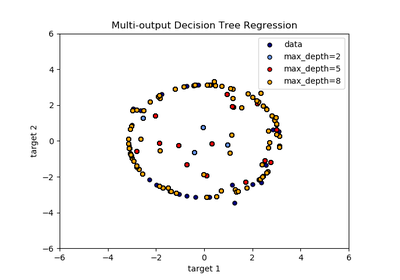
`sklearn.tree`.DecisionTreeRegressor¶

class sklearn.tree.DecisionTreeRegressor(criterion=’mse’, splitter=’best’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, presort=False)[source]¶

A decision tree regressor.

Read more in the User Guide.

Parameters:

criterion : string, optional (default=”mse”)

The function to measure the quality of a split. Supported criteria are “mse” for the mean squared error, which is equal to variance reduction as feature selection criterion and minimizes the L2 loss using the mean of each terminal node, “friedman_mse”, which uses mean squared error with Friedman’s improvement score for potential splits, and “mae” for the mean absolute error, which minimizes the L1 loss using the median of each terminal node.

New in version 0.18: Mean Absolute Error (MAE) criterion.

splitter : string, optional (default=”best”)

The strategy used to choose the split at each node. Supported strategies are “best” to choose the best split and “random” to choose the best random split.

max_depth : int or None, optional (default=None)

The maximum depth of the tree. If None, then nodes are expanded until all leaves are pure or until all leaves contain less than min_samples_split samples.

min_samples_split : int, float, optional (default=2)

The minimum number of samples required to split an internal node:

If int, then consider min_samples_split as the minimum number.

If float, then min_samples_split is a percentage and ceil(min_samples_split * n_samples) are the minimum number of samples for each split.

Changed in version 0.18: Added float values for percentages.

min_samples_leaf : int, float, optional (default=1)

The minimum number of samples required to be at a leaf node:

If int, then consider min_samples_leaf as the minimum number.

If float, then min_samples_leaf is a percentage and ceil(min_samples_leaf * n_samples) are the minimum number of samples for each node.

Changed in version 0.18: Added float values for percentages.

min_weight_fraction_leaf : float, optional (default=0.)

The minimum weighted fraction of the sum total of weights (of all the input samples) required to be at a leaf node. Samples have equal weight when sample_weight is not provided.

max_features : int, float, string or None, optional (default=None)

The number of features to consider when looking for the best split:

If int, then consider max_features features at each split.

If float, then max_features is a percentage and int(max_features * n_features) features are considered at each split.

If “auto”, then max_features=n_features.

If “sqrt”, then max_features=sqrt(n_features).

If “log2”, then max_features=log2(n_features).

If None, then max_features=n_features.

Note: the search for a split does not stop until at least one valid partition of the node samples is found, even if it requires to effectively inspect more than max_features features.

random_state : int, RandomState instance or None, optional (default=None)

If int, random_state is the seed used by the random number generator; If RandomState instance, random_state is the random number generator; If None, the random number generator is the RandomState instance used by np.random.

max_leaf_nodes : int or None, optional (default=None)

Grow a tree with max_leaf_nodes in best-first fashion. Best nodes are defined as relative reduction in impurity. If None then unlimited number of leaf nodes.

min_impurity_decrease : float, optional (default=0.)

A node will be split if this split induces a decrease of the impurity greater than or equal to this value.

The weighted impurity decrease equation is the following:
N_t / N * (impurity - N_t_R / N_t * right_impurity
                    - N_t_L / N_t * left_impurity)
where N is the total number of samples, N_t is the number of samples at the current node, N_t_L is the number of samples in the left child, and N_t_R is the number of samples in the right child.

N, N_t, N_t_R and N_t_L all refer to the weighted sum, if sample_weight is passed.

New in version 0.19.

min_impurity_split : float,

Threshold for early stopping in tree growth. A node will split if its impurity is above the threshold, otherwise it is a leaf.

Deprecated since version 0.19: min_impurity_split has been deprecated in favor of min_impurity_decrease in 0.19 and will be removed in 0.21. Use min_impurity_decrease instead.

presort : bool, optional (default=False)

Whether to presort the data to speed up the finding of best splits in fitting. For the default settings of a decision tree on large datasets, setting this to true may slow down the training process. When using either a smaller dataset or a restricted depth, this may speed up the training.

Attributes:

feature_importances_ : array of shape = [n_features]

The feature importances. The higher, the more important the feature. The importance of a feature is computed as the (normalized) total reduction of the criterion brought by that feature. It is also known as the Gini importance [R255].

max_features_ : int,

The inferred value of max_features.

n_features_ : int

The number of features when fit is performed.

n_outputs_ : int

The number of outputs when fit is performed.

tree_ : Tree object

The underlying Tree object.

See also

DecisionTreeClassifier

Notes

The default values for the parameters controlling the size of the trees (e.g. max_depth, min_samples_leaf, etc.) lead to fully grown and unpruned trees which can potentially be very large on some data sets. To reduce memory consumption, the complexity and size of the trees should be controlled by setting those parameter values.

The features are always randomly permuted at each split. Therefore, the best found split may vary, even with the same training data and max_features=n_features, if the improvement of the criterion is identical for several splits enumerated during the search of the best split. To obtain a deterministic behaviour during fitting, random_state has to be fixed.

References

[R252]

https://en.wikipedia.org/wiki/Decision_tree_learning

[R253]

L. Breiman, J. Friedman, R. Olshen, and C. Stone, “Classification and Regression Trees”, Wadsworth, Belmont, CA, 1984.

[R254]

T. Hastie, R. Tibshirani and J. Friedman. “Elements of Statistical Learning”, Springer, 2009.

[R255]

(1, 2) L. Breiman, and A. Cutler, “Random Forests”, http://www.stat.berkeley.edu/~breiman/RandomForests/cc_home.htm

Examples

>>> from sklearn.datasets import load_boston
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.tree import DecisionTreeRegressor
>>> boston = load_boston()
>>> regressor = DecisionTreeRegressor(random_state=0)
>>> cross_val_score(regressor, boston.data, boston.target, cv=10)
...                    
...
array([ 0.61..., 0.57..., -0.34..., 0.41..., 0.75...,
        0.07..., 0.29..., 0.33..., -1.42..., -1.77...])

Methods

`apply`(X[, check_input])	Returns the index of the leaf that each sample is predicted as.
`decision_path`(X[, check_input])	Return the decision path in the tree
`fit`(X, y[, sample_weight, check_input, …])	Build a decision tree regressor from the training set (X, y).
`get_params`([deep])	Get parameters for this estimator.
`predict`(X[, check_input])	Predict class or regression value for X.
`score`(X, y[, sample_weight])	Returns the coefficient of determination R^2 of the prediction.
`set_params`(**params)	Set the parameters of this estimator.

__init__(criterion=’mse’, splitter=’best’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, presort=False)[source]¶

apply(X, check_input=True)[source]¶

Returns the index of the leaf that each sample is predicted as.

New in version 0.17.

Parameters:

X : array_like or sparse matrix, shape = [n_samples, n_features]

The input samples. Internally, it will be converted to dtype=np.float32 and if a sparse matrix is provided to a sparse csr_matrix.

check_input : boolean, (default=True)

Allow to bypass several input checking. Don’t use this parameter unless you know what you do.

Returns:

X_leaves : array_like, shape = [n_samples,]

For each datapoint x in X, return the index of the leaf x ends up in. Leaves are numbered within [0; self.tree_.node_count), possibly with gaps in the numbering.

decision_path(X, check_input=True)[source]¶

Return the decision path in the tree

New in version 0.18.

Parameters:

X : array_like or sparse matrix, shape = [n_samples, n_features]

The input samples. Internally, it will be converted to dtype=np.float32 and if a sparse matrix is provided to a sparse csr_matrix.

check_input : boolean, (default=True)

Allow to bypass several input checking. Don’t use this parameter unless you know what you do.

Returns:

indicator : sparse csr array, shape = [n_samples, n_nodes]

Return a node indicator matrix where non zero elements indicates that the samples goes through the nodes.

feature_importances_¶

Return the feature importances.

The importance of a feature is computed as the (normalized) total reduction of the criterion brought by that feature. It is also known as the Gini importance.

Returns:	feature_importances_ : array, shape = [n_features]

fit(X, y, sample_weight=None, check_input=True, X_idx_sorted=None)[source]¶

Build a decision tree regressor from the training set (X, y).

Parameters:

X : array-like or sparse matrix, shape = [n_samples, n_features]

The training input samples. Internally, it will be converted to dtype=np.float32 and if a sparse matrix is provided to a sparse csc_matrix.

y : array-like, shape = [n_samples] or [n_samples, n_outputs]

The target values (real numbers). Use dtype=np.float64 and order='C' for maximum efficiency.

sample_weight : array-like, shape = [n_samples] or None

Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node.

check_input : boolean, (default=True)

Allow to bypass several input checking. Don’t use this parameter unless you know what you do.

X_idx_sorted : array-like, shape = [n_samples, n_features], optional

The indexes of the sorted training input samples. If many tree are grown on the same dataset, this allows the ordering to be cached between trees. If None, the data will be sorted here. Don’t use this parameter unless you know what to do.

Returns:

self : object

Returns self.

get_params(deep=True)[source]¶

Get parameters for this estimator.

Parameters:

deep : boolean, optional

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

params : mapping of string to any

Parameter names mapped to their values.

predict(X, check_input=True)[source]¶

Predict class or regression value for X.

For a classification model, the predicted class for each sample in X is returned. For a regression model, the predicted value based on X is returned.

Parameters:

X : array-like or sparse matrix of shape = [n_samples, n_features]

The input samples. Internally, it will be converted to dtype=np.float32 and if a sparse matrix is provided to a sparse csr_matrix.

check_input : boolean, (default=True)

Allow to bypass several input checking. Don’t use this parameter unless you know what you do.

Returns:

y : array of shape = [n_samples] or [n_samples, n_outputs]

The predicted classes, or the predict values.

score(X, y, sample_weight=None)[source]¶

Returns the coefficient of determination R^2 of the prediction.

The coefficient R^2 is defined as (1 - u/v), where u is the residual sum of squares ((y_true - y_pred) ** 2).sum() and v is the total sum of squares ((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a R^2 score of 0.0.

Parameters:

X : array-like, shape = (n_samples, n_features)

Test samples.

y : array-like, shape = (n_samples) or (n_samples, n_outputs)

True values for X.

sample_weight : array-like, shape = [n_samples], optional

Sample weights.

Returns:

score : float

R^2 of self.predict(X) wrt. y.

set_params(**params)[source]¶

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as pipelines). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.