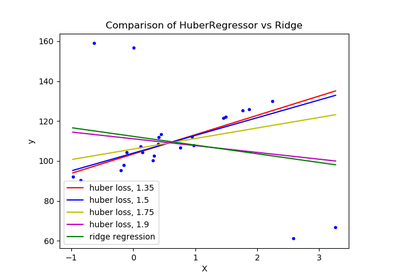
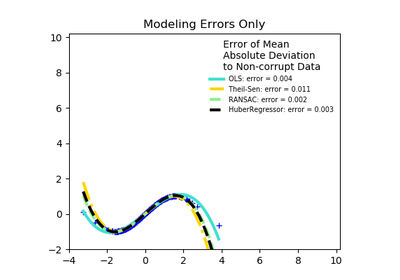
sklearn.linear_model.HuberRegressor¶
-
class
sklearn.linear_model.HuberRegressor(epsilon=1.35, max_iter=100, alpha=0.0001, warm_start=False, fit_intercept=True, tol=1e-05)[source]¶ Linear regression model that is robust to outliers.
The Huber Regressor optimizes the squared loss for the samples where
|(y - X'w) / sigma| < epsilonand the absolute loss for the samples where|(y - X'w) / sigma| > epsilon, where w and sigma are parameters to be optimized. The parameter sigma makes sure that if y is scaled up or down by a certain factor, one does not need to rescale epsilon to achieve the same robustness. Note that this does not take into account the fact that the different features of X may be of different scales.This makes sure that the loss function is not heavily influenced by the outliers while not completely ignoring their effect.
Read more in the User Guide
New in version 0.18.
Parameters: epsilon : float, greater than 1.0, default 1.35
The parameter epsilon controls the number of samples that should be classified as outliers. The smaller the epsilon, the more robust it is to outliers.
max_iter : int, default 100
Maximum number of iterations that scipy.optimize.fmin_l_bfgs_b should run for.
alpha : float, default 0.0001
Regularization parameter.
warm_start : bool, default False
This is useful if the stored attributes of a previously used model has to be reused. If set to False, then the coefficients will be rewritten for every call to fit.
fit_intercept : bool, default True
Whether or not to fit the intercept. This can be set to False if the data is already centered around the origin.
tol : float, default 1e-5
The iteration will stop when
max{|proj g_i | i = 1, ..., n}<=tolwhere pg_i is the i-th component of the projected gradient.Attributes: coef_ : array, shape (n_features,)
Features got by optimizing the Huber loss.
intercept_ : float
Bias.
scale_ : float
The value by which
|y - X'w - c|is scaled down.n_iter_ : int
Number of iterations that fmin_l_bfgs_b has run for.
Changed in version 0.20: In SciPy <= 1.0.0 the number of lbfgs iterations may exceed
max_iter.n_iter_will now report at mostmax_iter.outliers_ : array, shape (n_samples,)
A boolean mask which is set to True where the samples are identified as outliers.
References
[R180] Peter J. Huber, Elvezio M. Ronchetti, Robust Statistics Concomitant scale estimates, pg 172 [R181] Art B. Owen (2006), A robust hybrid of lasso and ridge regression. http://statweb.stanford.edu/~owen/reports/hhu.pdf Methods
fit(X, y[, sample_weight])Fit the model according to the given training data. get_params([deep])Get parameters for this estimator. predict(X)Predict using the linear model score(X, y[, sample_weight])Returns the coefficient of determination R^2 of the prediction. set_params(**params)Set the parameters of this estimator. -
__init__(epsilon=1.35, max_iter=100, alpha=0.0001, warm_start=False, fit_intercept=True, tol=1e-05)[source]¶
-
fit(X, y, sample_weight=None)[source]¶ Fit the model according to the given training data.
Parameters: X : array-like, shape (n_samples, n_features)
Training vector, where n_samples in the number of samples and n_features is the number of features.
y : array-like, shape (n_samples,)
Target vector relative to X.
sample_weight : array-like, shape (n_samples,)
Weight given to each sample.
Returns: self : object
Returns self.
-
get_params(deep=True)[source]¶ Get parameters for this estimator.
Parameters: deep : boolean, optional
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns: params : mapping of string to any
Parameter names mapped to their values.
-
predict(X)[source]¶ Predict using the linear model
Parameters: X : {array-like, sparse matrix}, shape = (n_samples, n_features)
Samples.
Returns: C : array, shape = (n_samples,)
Returns predicted values.
-
score(X, y, sample_weight=None)[source]¶ Returns the coefficient of determination R^2 of the prediction.
The coefficient R^2 is defined as (1 - u/v), where u is the residual sum of squares ((y_true - y_pred) ** 2).sum() and v is the total sum of squares ((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a R^2 score of 0.0.
Parameters: X : array-like, shape = (n_samples, n_features)
Test samples.
y : array-like, shape = (n_samples) or (n_samples, n_outputs)
True values for X.
sample_weight : array-like, shape = [n_samples], optional
Sample weights.
Returns: score : float
R^2 of self.predict(X) wrt. y.
-
set_params(**params)[source]¶ Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as pipelines). The latter have parameters of the form
<component>__<parameter>so that it’s possible to update each component of a nested object.Returns: self :
-