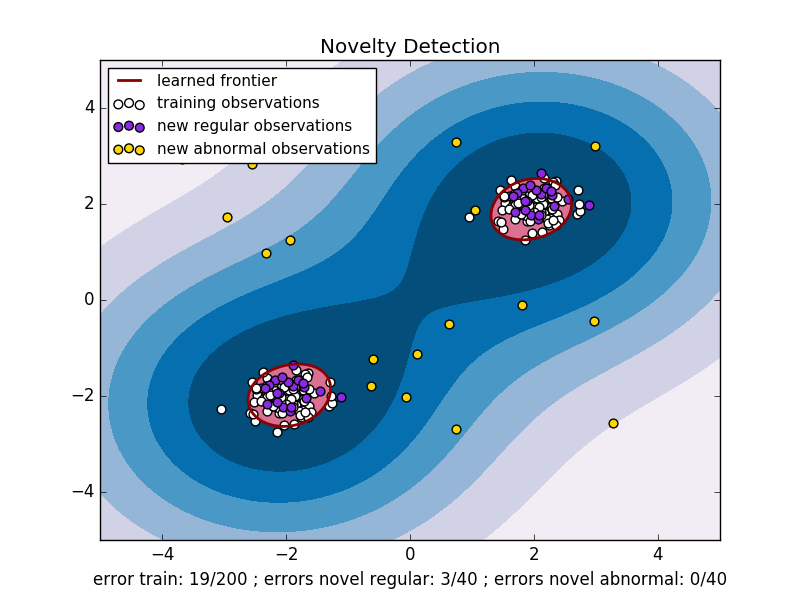
2.7. Novelty and Outlier Detection

Many applications require being able to decide whether a new observation belongs to the same distribution as existing observations (it is an inlier), or should be considered as different (it is an outlier). Often, this ability is used to clean real data sets. Two important distinction must be made:

novelty detection:  The training data is not polluted by outliers, and we are interested in detecting anomalies in new observations. outlier detection:  The training data contains outliers, and we need to fit the central mode of the training data, ignoring the deviant observations.

The scikit-learn project provides a set of machine learning tools that can be used both for novelty or outliers detection. This strategy is implemented with objects learning in an unsupervised way from the data:

estimator.fit(X_train)

new observations can then be sorted as inliers or outliers with a predict method:

estimator.predict(X_test)

Inliers are labeled 1, while outliers are labeled -1.

2.7.1. Novelty Detection

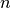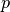Consider a data set of observations from the same distribution described by features. Consider now that we add one more observation to that data set. Is the new observation so different from the others that we can doubt it is regular? (i.e. does it come from the same distribution?) Or on the contrary, is it so similar to the other that we cannot distinguish it from the original observations? This is the question addressed by the novelty detection tools and methods.

In general, it is about to learn a rough, close frontier delimiting the contour of the initial observations distribution, plotted in embedding 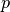-dimensional space. Then, if further observations lay within the frontier-delimited subspace, they are considered as coming from the same population than the initial observations. Otherwise, if they lay outside the frontier, we can say that they are abnormal with a given confidence in our assessment.

The One-Class SVM has been introduced by Schölkopf et al. for that purpose and implemented in the Support Vector Machines module in the svm.OneClassSVM object. It requires the choice of a kernel and a scalar parameter to define a frontier. The RBF kernel is usually chosen although there exists no exact formula or algorithm to set its bandwidth parameter. This is the default in the scikit-learn implementation. The 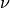parameter, also known as the margin of the One-Class SVM, corresponds to the probability of finding a new, but regular, observation outside the frontier.

References:

• Estimating the support of a high-dimensional distribution Schölkopf, Bernhard, et al. Neural computation 13.7 (2001): 1443-1471.

Examples:

• See One-class SVM with non-linear kernel (RBF) for visualizing the frontier learned around some data by a svm.OneClassSVM object.

2.7.2. Outlier Detection

Outlier detection is similar to novelty detection in the sense that the goal is to separate a core of regular observations from some polluting ones, called “outliers”. Yet, in the case of outlier detection, we don’t have a clean data set representing the population of regular observations that can be used to train any tool.

2.7.2.1. Fitting an elliptic envelope

One common way of performing outlier detection is to assume that the regular data come from a known distribution (e.g. data are Gaussian distributed). From this assumption, we generally try to define the “shape” of the data, and can define outlying observations as observations which stand far enough from the fit shape.

The scikit-learn provides an object covariance.EllipticEnvelope that fits a robust covariance estimate to the data, and thus fits an ellipse to the central data points, ignoring points outside the central mode.

For instance, assuming that the inlier data are Gaussian distributed, it will estimate the inlier location and covariance in a robust way (i.e. whithout being influenced by outliers). The Mahalanobis distances obtained from this estimate is used to derive a measure of outlyingness. This strategy is illustrated below.

Examples:

• See Robust covariance estimation and Mahalanobis distances relevance for an illustration of the difference between using a standard (covariance.EmpiricalCovariance) or a robust estimate (covariance.MinCovDet) of location and covariance to assess the degree of outlyingness of an observation.

References:

[RD1999]

Rousseeuw, P.J., Van Driessen, K. “A fast algorithm for the minimum covariance determinant estimator” Technometrics 41(3), 212 (1999)

2.7.2.2. Isolation Forest

One efficient way of performing outlier detection in high-dimensional datasets is to use random forests. The ensemble.IsolationForest ‘isolates’ observations by randomly selecting a feature and then randomly selecting a split value between the maximum and minimum values of the selected feature.

Since recursive partitioning can be represented by a tree structure, the number of splittings required to isolate a sample is equivalent to the path length from the root node to the terminating node.

This path length, averaged over a forest of such random trees, is a measure of normality and our decision function.

Random partitioning produces noticeably shorter paths for anomalies. Hence, when a forest of random trees collectively produce shorter path lengths for particular samples, they are highly likely to be anomalies.

This strategy is illustrated below.

Examples:

• See IsolationForest example for an illustration of the use of IsolationForest.
• See Outlier detection with several methods. for a comparison of ensemble.IsolationForest with svm.OneClassSVM (tuned to perform like an outlier detection method) and a covariance-based outlier detection with covariance.MinCovDet.

References:

[LTZ2008]

Liu, Fei Tony, Ting, Kai Ming and Zhou, Zhi-Hua. “Isolation forest.” Data Mining, 2008. ICDM‘08. Eighth IEEE International Conference on.

2.7.2.3. One-class SVM versus Elliptic Envelope versus Isolation Forest

Strictly-speaking, the One-class SVM is not an outlier-detection method, but a novelty-detection method: its training set should not be contaminated by outliers as it may fit them. That said, outlier detection in high-dimension, or without any assumptions on the distribution of the inlying data is very challenging, and a One-class SVM gives useful results in these situations.

The examples below illustrate how the performance of the covariance.EllipticEnvelope degrades as the data is less and less unimodal. The svm.OneClassSVM works better on data with multiple modes and ensemble.IsolationForest performs well in every cases.

Comparing One-class SVM approach, and elliptic envelope

For a inlier mode well-centered and elliptic, the svm.OneClassSVM is not able to benefit from the rotational symmetry of the inlier population. In addition, it fits a bit the outliers present in the training set. On the opposite, the decision rule based on fitting an covariance.EllipticEnvelope learns an ellipse, which fits well the inlier distribution. The ensemble.IsolationForest performs as well.
As the inlier distribution becomes bimodal, the covariance.EllipticEnvelope does not fit well the inliers. However, we can see that both ensemble.IsolationForest and svm.OneClassSVM have difficulties to detect the two modes, and that the svm.OneClassSVM tends to overfit: because it has not model of inliers, it interprets a region where, by chance some outliers are clustered, as inliers.
If the inlier distribution is strongly non Gaussian, the svm.OneClassSVM is able to recover a reasonable approximation as well as ensemble.IsolationForest, whereas the covariance.EllipticEnvelope completely fails.

Examples:

• See Outlier detection with several methods. for a comparison of the svm.OneClassSVM (tuned to perform like an outlier detection method), the ensemble.IsolationForest and a covariance-based outlier detection with covariance.MinCovDet.