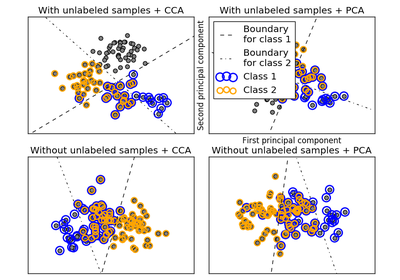
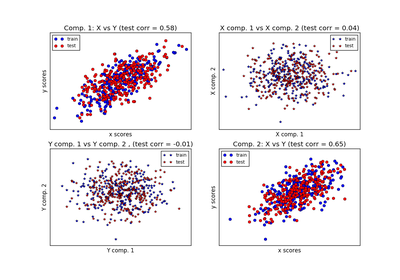
sklearn.cross_decomposition.CCA¶
-
class
sklearn.cross_decomposition.CCA(n_components=2, scale=True, max_iter=500, tol=1e-06, copy=True)[source]¶ CCA Canonical Correlation Analysis.
CCA inherits from PLS with mode=”B” and deflation_mode=”canonical”.
Read more in the User Guide.
Parameters: n_components : int, (default 2).
number of components to keep.
scale : boolean, (default True)
whether to scale the data?
max_iter : an integer, (default 500)
the maximum number of iterations of the NIPALS inner loop
tol : non-negative real, default 1e-06.
the tolerance used in the iterative algorithm
copy : boolean
Whether the deflation be done on a copy. Let the default value to True unless you don’t care about side effects
Attributes: x_weights_ : array, [p, n_components]
X block weights vectors.
y_weights_ : array, [q, n_components]
Y block weights vectors.
x_loadings_ : array, [p, n_components]
X block loadings vectors.
y_loadings_ : array, [q, n_components]
Y block loadings vectors.
x_scores_ : array, [n_samples, n_components]
X scores.
y_scores_ : array, [n_samples, n_components]
Y scores.
x_rotations_ : array, [p, n_components]
X block to latents rotations.
y_rotations_ : array, [q, n_components]
Y block to latents rotations.
n_iter_ : array-like
Number of iterations of the NIPALS inner loop for each component.
See also
Notes
For each component k, find the weights u, v that maximizes max corr(Xk u, Yk v), such that
|u| = |v| = 1Note that it maximizes only the correlations between the scores.
The residual matrix of X (Xk+1) block is obtained by the deflation on the current X score: x_score.
The residual matrix of Y (Yk+1) block is obtained by deflation on the current Y score.
References
Jacob A. Wegelin. A survey of Partial Least Squares (PLS) methods, with emphasis on the two-block case. Technical Report 371, Department of Statistics, University of Washington, Seattle, 2000.
In french but still a reference: Tenenhaus, M. (1998). La regression PLS: theorie et pratique. Paris: Editions Technic.
Examples
>>> from sklearn.cross_decomposition import CCA >>> X = [[0., 0., 1.], [1.,0.,0.], [2.,2.,2.], [3.,5.,4.]] >>> Y = [[0.1, -0.2], [0.9, 1.1], [6.2, 5.9], [11.9, 12.3]] >>> cca = CCA(n_components=1) >>> cca.fit(X, Y) ... CCA(copy=True, max_iter=500, n_components=1, scale=True, tol=1e-06) >>> X_c, Y_c = cca.transform(X, Y)
Methods
fit(X, Y)Fit model to data. fit_transform(X[, y])Learn and apply the dimension reduction on the train data. get_params([deep])Get parameters for this estimator. predict(X[, copy])Apply the dimension reduction learned on the train data. score(X, y[, sample_weight])Returns the coefficient of determination R^2 of the prediction. set_params(\*\*params)Set the parameters of this estimator. transform(X[, Y, copy])Apply the dimension reduction learned on the train data. -
fit(X, Y)[source]¶ Fit model to data.
Parameters: X : array-like, shape = [n_samples, n_features]
Training vectors, where n_samples in the number of samples and n_features is the number of predictors.
Y : array-like of response, shape = [n_samples, n_targets]
Target vectors, where n_samples in the number of samples and n_targets is the number of response variables.
-
fit_transform(X, y=None, **fit_params)[source]¶ Learn and apply the dimension reduction on the train data.
Parameters: X : array-like of predictors, shape = [n_samples, p]
Training vectors, where n_samples in the number of samples and p is the number of predictors.
Y : array-like of response, shape = [n_samples, q], optional
Training vectors, where n_samples in the number of samples and q is the number of response variables.
copy : boolean, default True
Whether to copy X and Y, or perform in-place normalization.
Returns: x_scores if Y is not given, (x_scores, y_scores) otherwise. :
-
get_params(deep=True)[source]¶ Get parameters for this estimator.
Parameters: deep : boolean, optional
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns: params : mapping of string to any
Parameter names mapped to their values.
-
predict(X, copy=True)[source]¶ Apply the dimension reduction learned on the train data.
Parameters: X : array-like of predictors, shape = [n_samples, p]
Training vectors, where n_samples in the number of samples and p is the number of predictors.
copy : boolean, default True
Whether to copy X and Y, or perform in-place normalization.
Notes
This call requires the estimation of a p x q matrix, which may be an issue in high dimensional space.
-
score(X, y, sample_weight=None)[source]¶ Returns the coefficient of determination R^2 of the prediction.
The coefficient R^2 is defined as (1 - u/v), where u is the regression sum of squares ((y_true - y_pred) ** 2).sum() and v is the residual sum of squares ((y_true - y_true.mean()) ** 2).sum(). Best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a R^2 score of 0.0.
Parameters: X : array-like, shape = (n_samples, n_features)
Test samples.
y : array-like, shape = (n_samples) or (n_samples, n_outputs)
True values for X.
sample_weight : array-like, shape = [n_samples], optional
Sample weights.
Returns: score : float
R^2 of self.predict(X) wrt. y.
-
set_params(**params)[source]¶ Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as pipelines). The latter have parameters of the form
<component>__<parameter>so that it’s possible to update each component of a nested object.Returns: self :
-
transform(X, Y=None, copy=True)[source]¶ Apply the dimension reduction learned on the train data.
Parameters: X : array-like of predictors, shape = [n_samples, p]
Training vectors, where n_samples in the number of samples and p is the number of predictors.
Y : array-like of response, shape = [n_samples, q], optional
Training vectors, where n_samples in the number of samples and q is the number of response variables.
copy : boolean, default True
Whether to copy X and Y, or perform in-place normalization.
Returns: x_scores if Y is not given, (x_scores, y_scores) otherwise. :
-