SVM Exercise

A tutorial exercise for using different SVM kernels.

This exercise is used in the Using kernels part of the Supervised learning: predicting an output variable from high-dimensional observations section of the A tutorial on statistical-learning for scientific data processing.

• 
• 
• 

print(__doc__)


import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets, svm

iris = datasets.load_iris()
X = iris.data
y = iris.target

X = X[y != 0, :2]
y = y[y != 0]

n_sample = len(X)

np.random.seed(0)
order = np.random.permutation(n_sample)
X = X[order]
y = y[order].astype(np.float)

X_train = X[:int(.9 * n_sample)]
y_train = y[:int(.9 * n_sample)]
X_test = X[int(.9 * n_sample):]
y_test = y[int(.9 * n_sample):]

# fit the model
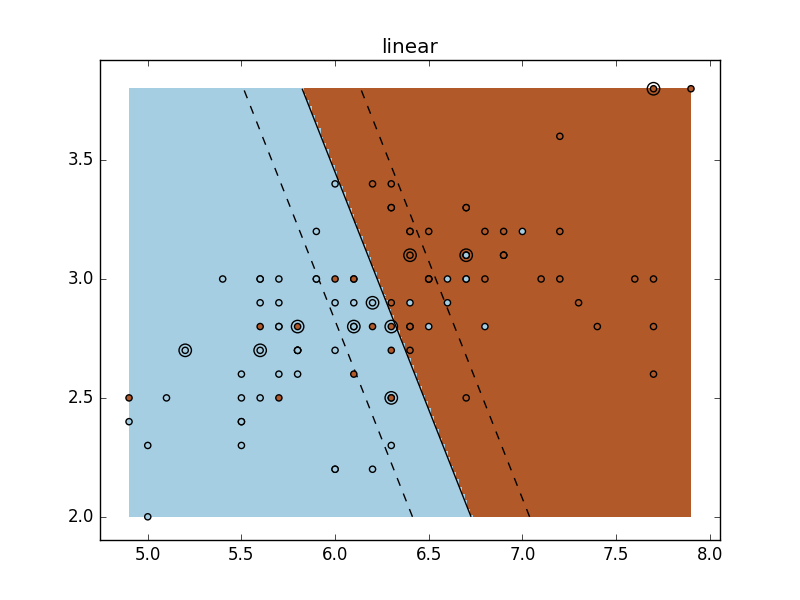
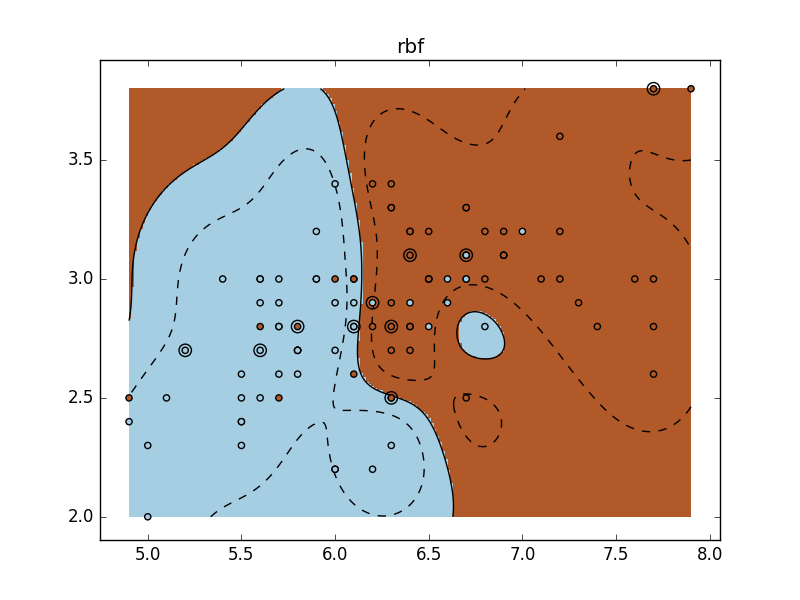
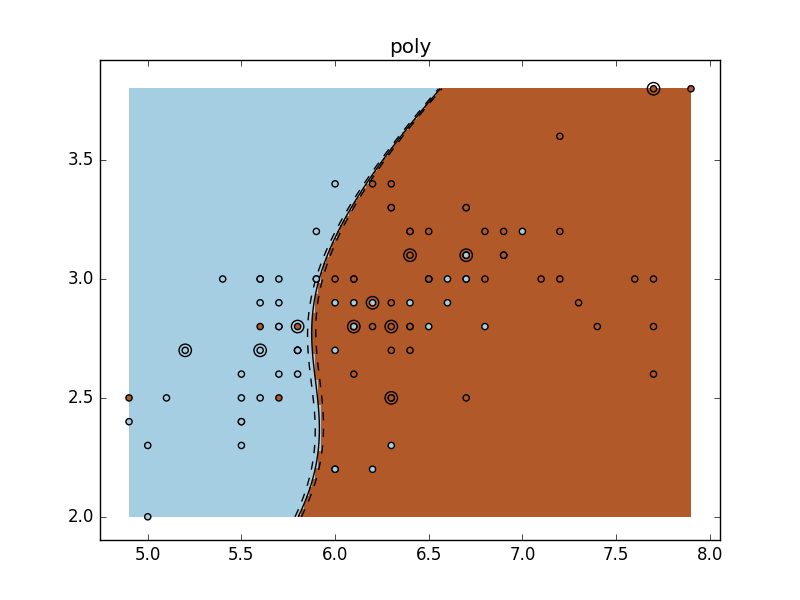
for fig_num, kernel in enumerate(('linear', 'rbf', 'poly')):
    clf = svm.SVC(kernel=kernel, gamma=10)
    clf.fit(X_train, y_train)

    plt.figure(fig_num)
    plt.clf()
    plt.scatter(X[:, 0], X[:, 1], c=y, zorder=10, cmap=plt.cm.Paired)

    # Circle out the test data
    plt.scatter(X_test[:, 0], X_test[:, 1], s=80, facecolors='none', zorder=10)

    plt.axis('tight')
    x_min = X[:, 0].min()
    x_max = X[:, 0].max()
    y_min = X[:, 1].min()
    y_max = X[:, 1].max()

    XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
    Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()])

    # Put the result into a color plot
    Z = Z.reshape(XX.shape)
    plt.pcolormesh(XX, YY, Z > 0, cmap=plt.cm.Paired)
    plt.contour(XX, YY, Z, colors=['k', 'k', 'k'],
                linestyles=['--', '-', '--'], levels=[-.5, 0, .5])

    plt.title(kernel)
plt.show()

Total running time of the script: (0 minutes 6.988 seconds)

Download Python source code: plot_iris_exercise.py

Download IPython notebook: plot_iris_exercise.ipynb