sklearn.manifold.MDS

class sklearn.manifold.MDS(n_components=2, metric=True, n_init=4, max_iter=300, verbose=0, eps=0.001, n_jobs=1, random_state=None, dissimilarity='euclidean')

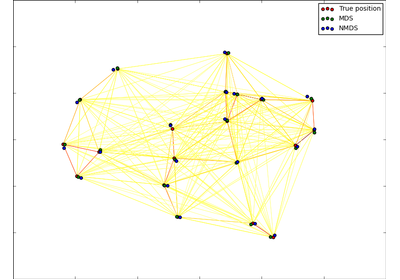
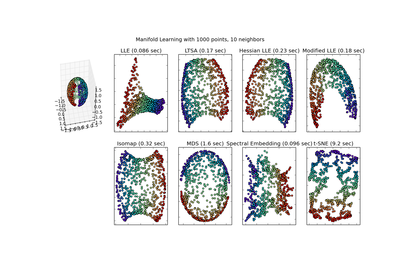
Multidimensional scaling

Parameters:

metric : boolean, optional, default: True

compute metric or nonmetric SMACOF (Scaling by Majorizing a Complicated Function) algorithm

n_components : int, optional, default: 2

number of dimension in which to immerse the similarities overridden if initial array is provided.

n_init : int, optional, default: 4

Number of time the smacof algorithm will be run with different initialisation. The final results will be the best output of the n_init consecutive runs in terms of stress.

max_iter : int, optional, default: 300

Maximum number of iterations of the SMACOF algorithm for a single run

verbose : int, optional, default: 0

level of verbosity

eps : float, optional, default: 1e-6

relative tolerance w.r.t stress to declare converge

n_jobs : int, optional, default: 1

The number of jobs to use for the computation. This works by breaking down the pairwise matrix into n_jobs even slices and computing them in parallel.

If -1 all CPUs are used. If 1 is given, no parallel computing code is used at all, which is useful for debugging. For n_jobs below -1, (n_cpus + 1 + n_jobs) are used. Thus for n_jobs = -2, all CPUs but one are used.

random_state : integer or numpy.RandomState, optional

The generator used to initialize the centers. If an integer is given, it fixes the seed. Defaults to the global numpy random number generator.

dissimilarity : string

Which dissimilarity measure to use. Supported are ‘euclidean’ and ‘precomputed’.

Attributes:

embedding_ : array-like, shape [n_components, n_samples]

Stores the position of the dataset in the embedding space

stress_ : float

The final value of the stress (sum of squared distance of the disparities and the distances for all constrained points)

References

“Modern Multidimensional Scaling - Theory and Applications” Borg, I.; Groenen P. Springer Series in Statistics (1997)

“Nonmetric multidimensional scaling: a numerical method” Kruskal, J. Psychometrika, 29 (1964)

“Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis” Kruskal, J. Psychometrika, 29, (1964)

Methods

fit(X[, y, init])	Computes the position of the points in the embedding space
fit_transform(X[, y, init])	Fit the data from X, and returns the embedded coordinates
get_params([deep])	Get parameters for this estimator.
set_params(**params)	Set the parameters of this estimator.

__init__(n_components=2, metric=True, n_init=4, max_iter=300, verbose=0, eps=0.001, n_jobs=1, random_state=None, dissimilarity='euclidean')

fit(X, y=None, init=None)

Computes the position of the points in the embedding space

Parameters:

X : array, shape=[n_samples, n_features], or [n_samples, n_samples] if dissimilarity=’precomputed’

Input data.

init : {None or ndarray, shape (n_samples,)}, optional

If None, randomly chooses the initial configuration if ndarray, initialize the SMACOF algorithm with this array.

fit_transform(X, y=None, init=None)

Fit the data from X, and returns the embedded coordinates

Parameters:

X : array, shape=[n_samples, n_features], or [n_samples, n_samples] if dissimilarity=’precomputed’

Input data.

init : {None or ndarray, shape (n_samples,)}, optional

If None, randomly chooses the initial configuration if ndarray, initialize the SMACOF algorithm with this array.

get_params(deep=True)

Get parameters for this estimator.

Parameters:

deep: boolean, optional :

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

params : mapping of string to any

Parameter names mapped to their values.

set_params(**params)

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as pipelines). The former have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Returns:self :

Examples using sklearn.manifold.MDS

Multi-dimensional scaling

Comparison of Manifold Learning methods

Manifold Learning methods on a severed sphere

Manifold learning on handwritten digits: Locally Linear Embedding, Isomap...