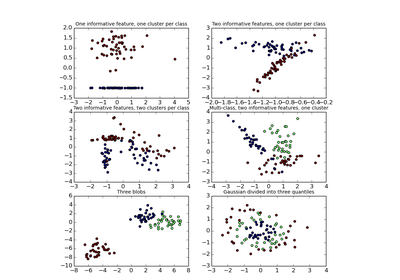
sklearn.datasets.make_classification¶
- sklearn.datasets.make_classification(n_samples=100, n_features=20, n_informative=2, n_redundant=2, n_repeated=0, n_classes=2, n_clusters_per_class=2, weights=None, flip_y=0.01, class_sep=1.0, hypercube=True, shift=0.0, scale=1.0, shuffle=True, random_state=None)[source]¶
Generate a random n-class classification problem.
This initially creates clusters of points normally distributed (std=1) about vertices of a 2 * class_sep-sided hypercube, and assigns an equal number of clusters to each class. It introduces interdependence between these features and adds various types of further noise to the data.
Prior to shuffling, X stacks a number of these primary “informative” features, “redundant” linear combinations of these, “repeated” duplicates of sampled features, and arbitrary noise for and remaining features.
Parameters: n_samples : int, optional (default=100)
The number of samples.
n_features : int, optional (default=20)
The total number of features. These comprise n_informative informative features, n_redundant redundant features, n_repeated duplicated features and n_features-n_informative-n_redundant- n_repeated useless features drawn at random.
n_informative : int, optional (default=2)
The number of informative features. Each class is composed of a number of gaussian clusters each located around the vertices of a hypercube in a subspace of dimension n_informative. For each cluster, informative features are drawn independently from N(0, 1) and then randomly linearly combined within each cluster in order to add covariance. The clusters are then placed on the vertices of the hypercube.
n_redundant : int, optional (default=2)
The number of redundant features. These features are generated as random linear combinations of the informative features.
n_repeated : int, optional (default=0)
The number of duplicated features, drawn randomly from the informative and the redundant features.
n_classes : int, optional (default=2)
The number of classes (or labels) of the classification problem.
n_clusters_per_class : int, optional (default=2)
The number of clusters per class.
weights : list of floats or None (default=None)
The proportions of samples assigned to each class. If None, then classes are balanced. Note that if len(weights) == n_classes - 1, then the last class weight is automatically inferred. More than n_samples samples may be returned if the sum of weights exceeds 1.
flip_y : float, optional (default=0.01)
The fraction of samples whose class are randomly exchanged.
class_sep : float, optional (default=1.0)
The factor multiplying the hypercube dimension.
hypercube : boolean, optional (default=True)
If True, the clusters are put on the vertices of a hypercube. If False, the clusters are put on the vertices of a random polytope.
shift : float, array of shape [n_features] or None, optional (default=0.0)
Shift features by the specified value. If None, then features are shifted by a random value drawn in [-class_sep, class_sep].
scale : float, array of shape [n_features] or None, optional (default=1.0)
Multiply features by the specified value. If None, then features are scaled by a random value drawn in [1, 100]. Note that scaling happens after shifting.
shuffle : boolean, optional (default=True)
Shuffle the samples and the features.
random_state : int, RandomState instance or None, optional (default=None)
If int, random_state is the seed used by the random number generator; If RandomState instance, random_state is the random number generator; If None, the random number generator is the RandomState instance used by np.random.
Returns: X : array of shape [n_samples, n_features]
The generated samples.
y : array of shape [n_samples]
The integer labels for class membership of each sample.
See also
- make_blobs
- simplified variant
- make_multilabel_classification
- unrelated generator for multilabel tasks
Notes
The algorithm is adapted from Guyon [1] and was designed to generate the “Madelon” dataset.
References
[R109] I. Guyon, “Design of experiments for the NIPS 2003 variable selection benchmark”, 2003.