Note
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
Ordinary Least Squares and Ridge Regression Variance¶
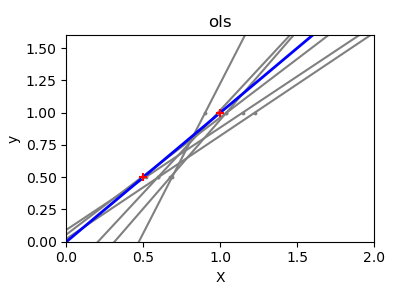
Due to the few points in each dimension and the straight line that linear regression uses to follow these points as well as it can, noise on the observations will cause great variance as shown in the first plot. Every line’s slope can vary quite a bit for each prediction due to the noise induced in the observations.
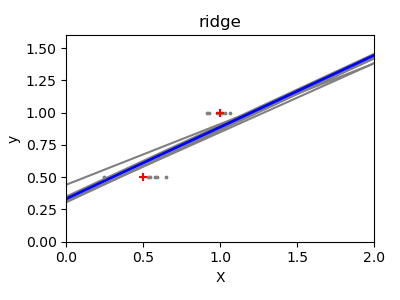
Ridge regression is basically minimizing a penalised version
of the least-squared function. The penalising shrinks the
value of the regression coefficients.
Despite the few data points in each dimension, the slope
of the prediction is much more stable and the variance
in the line itself is greatly reduced, in comparison to that
of the standard linear regression
# Code source: Gaël Varoquaux
# Modified for documentation by Jaques Grobler
# License: BSD 3 clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
X_train = np.c_[0.5, 1].T
y_train = [0.5, 1]
X_test = np.c_[0, 2].T
np.random.seed(0)
classifiers = dict(
ols=linear_model.LinearRegression(), ridge=linear_model.Ridge(alpha=0.1)
)
for name, clf in classifiers.items():
fig, ax = plt.subplots(figsize=(4, 3))
for _ in range(6):
this_X = 0.1 * np.random.normal(size=(2, 1)) + X_train
clf.fit(this_X, y_train)
ax.plot(X_test, clf.predict(X_test), color="gray")
ax.scatter(this_X, y_train, s=3, c="gray", marker="o", zorder=10)
clf.fit(X_train, y_train)
ax.plot(X_test, clf.predict(X_test), linewidth=2, color="blue")
ax.scatter(X_train, y_train, s=30, c="red", marker="+", zorder=10)
ax.set_title(name)
ax.set_xlim(0, 2)
ax.set_ylim((0, 1.6))
ax.set_xlabel("X")
ax.set_ylabel("y")
fig.tight_layout()
plt.show()
Total running time of the script: (0 minutes 0.263 seconds)
Related examples
Plot Ridge coefficients as a function of the regularization
HuberRegressor vs Ridge on dataset with strong outliers