3.4. Validation curves: plotting scores to evaluate models¶
Every estimator has its advantages and drawbacks. Its generalization error can be decomposed in terms of bias, variance and noise. The bias of an estimator is its average error for different training sets. The variance of an estimator indicates how sensitive it is to varying training sets. Noise is a property of the data.
In the following plot, we see a function \(f(x) = \cos (\frac{3}{2} \pi x)\) and some noisy samples from that function. We use three different estimators to fit the function: linear regression with polynomial features of degree 1, 4 and 15. We see that the first estimator can at best provide only a poor fit to the samples and the true function because it is too simple (high bias), the second estimator approximates it almost perfectly and the last estimator approximates the training data perfectly but does not fit the true function very well, i.e. it is very sensitive to varying training data (high variance).
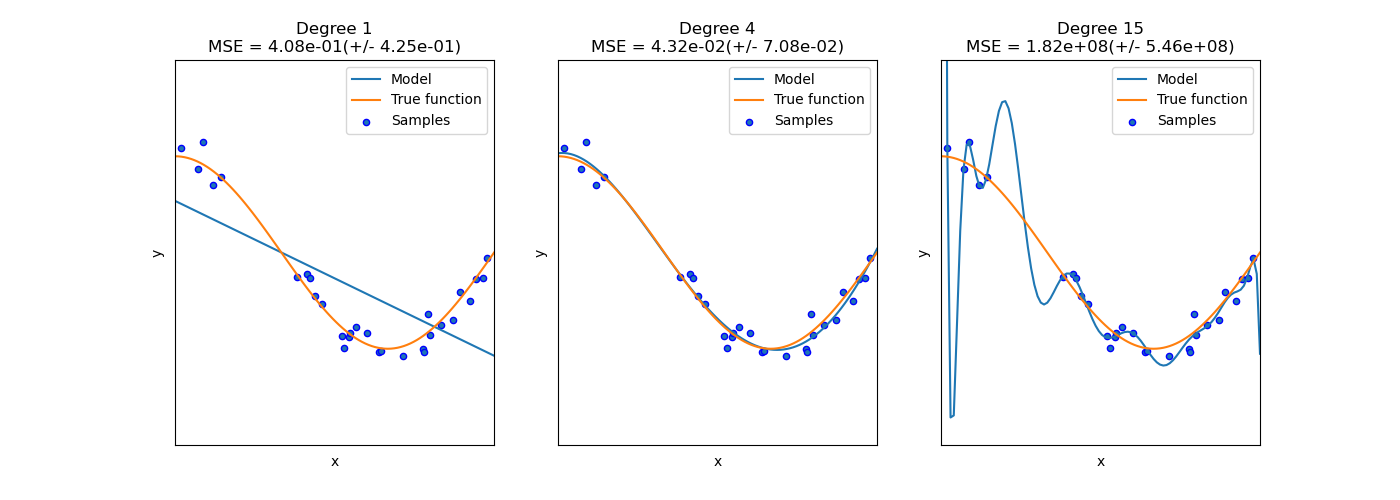
Bias and variance are inherent properties of estimators and we usually have to select learning algorithms and hyperparameters so that both bias and variance are as low as possible (see Bias-variance dilemma). Another way to reduce the variance of a model is to use more training data. However, you should only collect more training data if the true function is too complex to be approximated by an estimator with a lower variance.
In the simple one-dimensional problem that we have seen in the example it is easy to see whether the estimator suffers from bias or variance. However, in high-dimensional spaces, models can become very difficult to visualize. For this reason, it is often helpful to use the tools described below.
3.4.1. Validation curve¶
To validate a model we need a scoring function (see Metrics and scoring: quantifying the quality of predictions), for example accuracy for classifiers. The proper way of choosing multiple hyperparameters of an estimator is of course grid search or similar methods (see Tuning the hyper-parameters of an estimator) that select the hyperparameter with the maximum score on a validation set or multiple validation sets. Note that if we optimize the hyperparameters based on a validation score the validation score is biased and not a good estimate of the generalization any longer. To get a proper estimate of the generalization we have to compute the score on another test set.
However, it is sometimes helpful to plot the influence of a single hyperparameter on the training score and the validation score to find out whether the estimator is overfitting or underfitting for some hyperparameter values.
The function validation_curve can help in this case:
>>> import numpy as np
>>> from sklearn.model_selection import validation_curve
>>> from sklearn.datasets import load_iris
>>> from sklearn.linear_model import Ridge
>>> np.random.seed(0)
>>> X, y = load_iris(return_X_y=True)
>>> indices = np.arange(y.shape[0])
>>> np.random.shuffle(indices)
>>> X, y = X[indices], y[indices]
>>> train_scores, valid_scores = validation_curve(
... Ridge(), X, y, param_name="alpha", param_range=np.logspace(-7, 3, 3),
... cv=5)
>>> train_scores
array([[0.93..., 0.94..., 0.92..., 0.91..., 0.92...],
[0.93..., 0.94..., 0.92..., 0.91..., 0.92...],
[0.51..., 0.52..., 0.49..., 0.47..., 0.49...]])
>>> valid_scores
array([[0.90..., 0.84..., 0.94..., 0.96..., 0.93...],
[0.90..., 0.84..., 0.94..., 0.96..., 0.93...],
[0.46..., 0.25..., 0.50..., 0.49..., 0.52...]])
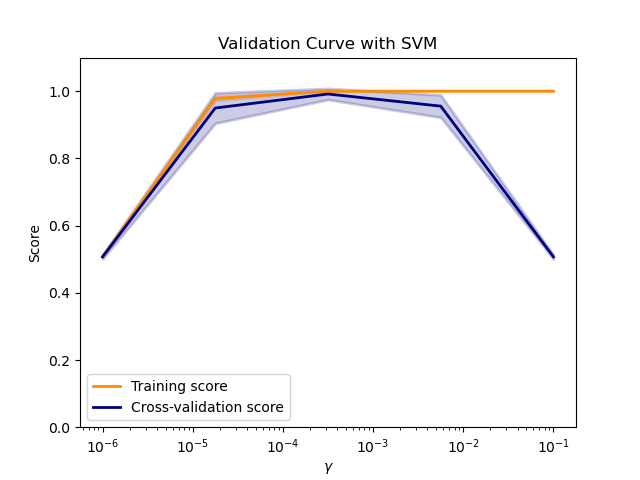
If the training score and the validation score are both low, the estimator will be underfitting. If the training score is high and the validation score is low, the estimator is overfitting and otherwise it is working very well. A low training score and a high validation score is usually not possible. Underfitting, overfitting, and a working model are shown in the in the plot below where we vary the parameter \(\gamma\) of an SVM on the digits dataset.
3.4.2. Learning curve¶
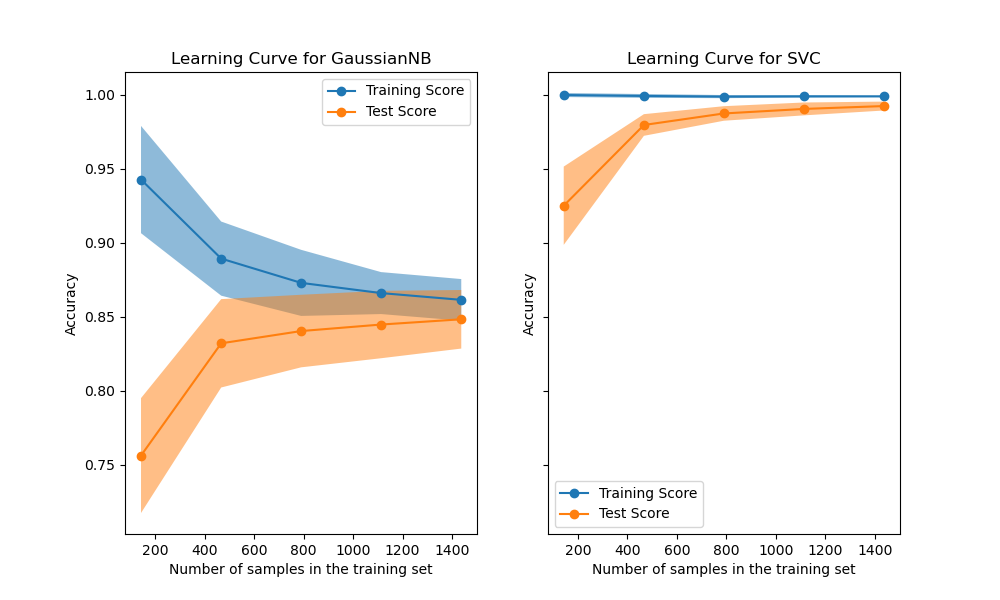
A learning curve shows the validation and training score of an estimator for varying numbers of training samples. It is a tool to find out how much we benefit from adding more training data and whether the estimator suffers more from a variance error or a bias error. Consider the following example where we plot the learning curve of a naive Bayes classifier and an SVM.
For the naive Bayes, both the validation score and the training score converge to a value that is quite low with increasing size of the training set. Thus, we will probably not benefit much from more training data.
In contrast, for small amounts of data, the training score of the SVM is much greater than the validation score. Adding more training samples will most likely increase generalization.
We can use the function learning_curve to generate the values
that are required to plot such a learning curve (number of samples
that have been used, the average scores on the training sets and the
average scores on the validation sets):
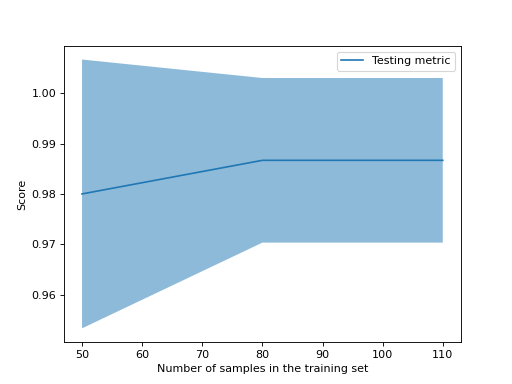
>>> from sklearn.model_selection import learning_curve
>>> from sklearn.svm import SVC
>>> train_sizes, train_scores, valid_scores = learning_curve(
... SVC(kernel='linear'), X, y, train_sizes=[50, 80, 110], cv=5)
>>> train_sizes
array([ 50, 80, 110])
>>> train_scores
array([[0.98..., 0.98 , 0.98..., 0.98..., 0.98...],
[0.98..., 1. , 0.98..., 0.98..., 0.98...],
[0.98..., 1. , 0.98..., 0.98..., 0.99...]])
>>> valid_scores
array([[1. , 0.93..., 1. , 1. , 0.96...],
[1. , 0.96..., 1. , 1. , 0.96...],
[1. , 0.96..., 1. , 1. , 0.96...]])
If you intend to plot the learning curves only, the class
LearningCurveDisplay will be easier to use.
You can use the method
from_estimator similarly
to learning_curve to generate and plot the learning curve:
from sklearn.datasets import load_iris
from sklearn.model_selection import LearningCurveDisplay
from sklearn.svm import SVC
from sklearn.utils import shuffle
X, y = load_iris(return_X_y=True)
X, y = shuffle(X, y, random_state=0)
LearningCurveDisplay.from_estimator(
SVC(kernel="linear"), X, y, train_sizes=[50, 80, 110], cv=5)