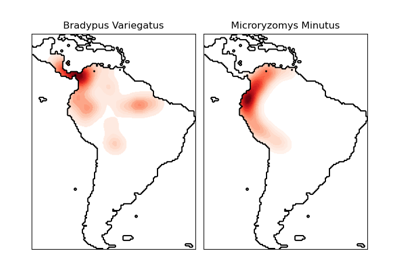
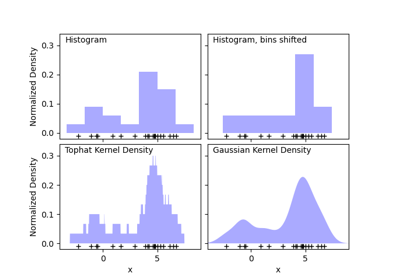
sklearn.neighbors.KernelDensity

class sklearn.neighbors.KernelDensity(*, bandwidth=1.0, algorithm='auto', kernel='gaussian', metric='euclidean', atol=0, rtol=0, breadth_first=True, leaf_size=40, metric_params=None)

Kernel Density Estimation.

Read more in the User Guide.

Parameters:

bandwidthfloat or {“scott”, “silverman”}, default=1.0

The bandwidth of the kernel. If bandwidth is a float, it defines the bandwidth of the kernel. If bandwidth is a string, one of the estimation methods is implemented.

algorithm{‘kd_tree’, ‘ball_tree’, ‘auto’}, default=’auto’

The tree algorithm to use.

kernel{‘gaussian’, ‘tophat’, ‘epanechnikov’, ‘exponential’, ‘linear’, ‘cosine’}, default=’gaussian’

The kernel to use.

metricstr, default=’euclidean’

Metric to use for distance computation. See the documentation of scipy.spatial.distance and the metrics listed in distance_metrics for valid metric values.

Not all metrics are valid with all algorithms: refer to the documentation of BallTree and KDTree. Note that the normalization of the density output is correct only for the Euclidean distance metric.

atolfloat, default=0

The desired absolute tolerance of the result. A larger tolerance will generally lead to faster execution.

rtolfloat, default=0

The desired relative tolerance of the result. A larger tolerance will generally lead to faster execution.

breadth_firstbool, default=True

If true (default), use a breadth-first approach to the problem. Otherwise use a depth-first approach.

leaf_sizeint, default=40

Specify the leaf size of the underlying tree. See BallTree or KDTree for details.

metric_paramsdict, default=None

Additional parameters to be passed to the tree for use with the metric. For more information, see the documentation of BallTree or KDTree.

Attributes:

n_features_in_int

Number of features seen during fit.

New in version 0.24.

tree_BinaryTree instance

The tree algorithm for fast generalized N-point problems.

feature_names_in_ndarray of shape (n_features_in_,)

Names of features seen during fit. Defined only when X has feature names that are all strings.

bandwidth_float

Value of the bandwidth, given directly by the bandwidth parameter or estimated using the ‘scott’ or ‘silverman’ method.

New in version 1.0.

See also

sklearn.neighbors.KDTree

K-dimensional tree for fast generalized N-point problems.

sklearn.neighbors.BallTree

Ball tree for fast generalized N-point problems.

Examples

Compute a gaussian kernel density estimate with a fixed bandwidth.

>>> from sklearn.neighbors import KernelDensity
>>> import numpy as np
>>> rng = np.random.RandomState(42)
>>> X = rng.random_sample((100, 3))
>>> kde = KernelDensity(kernel='gaussian', bandwidth=0.5).fit(X)
>>> log_density = kde.score_samples(X[:3])
>>> log_density
array([-1.52955942, -1.51462041, -1.60244657])

Methods

fit(X[, y, sample_weight])	Fit the Kernel Density model on the data.
get_params([deep])	Get parameters for this estimator.
sample([n_samples, random_state])	Generate random samples from the model.
score(X[, y])	Compute the total log-likelihood under the model.
score_samples(X)	Compute the log-likelihood of each sample under the model.
set_params(**params)	Set the parameters of this estimator.

fit(X, y=None, sample_weight=None)

Fit the Kernel Density model on the data.

Parameters:

Xarray-like of shape (n_samples, n_features)

List of n_features-dimensional data points. Each row corresponds to a single data point.

yNone

Ignored. This parameter exists only for compatibility with Pipeline.

sample_weightarray-like of shape (n_samples,), default=None

List of sample weights attached to the data X.

New in version 0.20.

Returns:

selfobject

Returns the instance itself.

get_params(deep=True)

Get parameters for this estimator.

Parameters:

deepbool, default=True

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict

Parameter names mapped to their values.

sample(n_samples=1, random_state=None)

Generate random samples from the model.

Currently, this is implemented only for gaussian and tophat kernels.

Parameters:

n_samplesint, default=1

Number of samples to generate.

random_stateint, RandomState instance or None, default=None

Determines random number generation used to generate random samples. Pass an int for reproducible results across multiple function calls. See Glossary.

Returns:

Xarray-like of shape (n_samples, n_features)

List of samples.

score(X, y=None)

Compute the total log-likelihood under the model.

Parameters:

Xarray-like of shape (n_samples, n_features)

List of n_features-dimensional data points. Each row corresponds to a single data point.

yNone

Ignored. This parameter exists only for compatibility with Pipeline.

Returns:

logprobfloat

Total log-likelihood of the data in X. This is normalized to be a probability density, so the value will be low for high-dimensional data.

score_samples(X)

Compute the log-likelihood of each sample under the model.

Parameters:

Xarray-like of shape (n_samples, n_features)

An array of points to query. Last dimension should match dimension of training data (n_features).

Returns:

densityndarray of shape (n_samples,)

Log-likelihood of each sample in X. These are normalized to be probability densities, so values will be low for high-dimensional data.

set_params(**params)

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict

Estimator parameters.

Returns:

selfestimator instance

Estimator instance.

Examples using sklearn.neighbors.KernelDensity

Kernel Density Estimate of Species Distributions

Kernel Density Estimate of Species Distributions

Kernel Density Estimation

Kernel Density Estimation

Simple 1D Kernel Density Estimation

Simple 1D Kernel Density Estimation