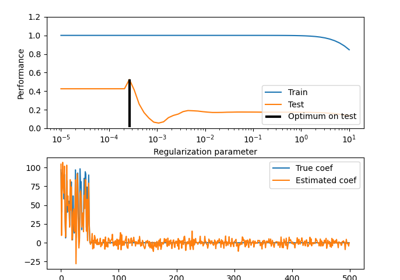
sklearn.datasets.make_regression¶
- sklearn.datasets.make_regression(n_samples=100, n_features=100, *, n_informative=10, n_targets=1, bias=0.0, effective_rank=None, tail_strength=0.5, noise=0.0, shuffle=True, coef=False, random_state=None)[source]¶
Generate a random regression problem.
The input set can either be well conditioned (by default) or have a low rank-fat tail singular profile. See
make_low_rank_matrixfor more details.The output is generated by applying a (potentially biased) random linear regression model with
n_informativenonzero regressors to the previously generated input and some gaussian centered noise with some adjustable scale.Read more in the User Guide.
- Parameters:
- n_samplesint, default=100
The number of samples.
- n_featuresint, default=100
The number of features.
- n_informativeint, default=10
The number of informative features, i.e., the number of features used to build the linear model used to generate the output.
- n_targetsint, default=1
The number of regression targets, i.e., the dimension of the y output vector associated with a sample. By default, the output is a scalar.
- biasfloat, default=0.0
The bias term in the underlying linear model.
- effective_rankint, default=None
- If not None:
The approximate number of singular vectors required to explain most of the input data by linear combinations. Using this kind of singular spectrum in the input allows the generator to reproduce the correlations often observed in practice.
- If None:
The input set is well conditioned, centered and gaussian with unit variance.
- tail_strengthfloat, default=0.5
The relative importance of the fat noisy tail of the singular values profile if
effective_rankis not None. When a float, it should be between 0 and 1.- noisefloat, default=0.0
The standard deviation of the gaussian noise applied to the output.
- shufflebool, default=True
Shuffle the samples and the features.
- coefbool, default=False
If True, the coefficients of the underlying linear model are returned.
- random_stateint, RandomState instance or None, default=None
Determines random number generation for dataset creation. Pass an int for reproducible output across multiple function calls. See Glossary.
- Returns:
- Xndarray of shape (n_samples, n_features)
The input samples.
- yndarray of shape (n_samples,) or (n_samples, n_targets)
The output values.
- coefndarray of shape (n_features,) or (n_features, n_targets)
The coefficient of the underlying linear model. It is returned only if coef is True.
Examples
>>> from sklearn.datasets import make_regression >>> X, y = make_regression(n_samples=5, n_features=2, noise=1, random_state=42) >>> X array([[ 0.4967..., -0.1382... ], [ 0.6476..., 1.523...], [-0.2341..., -0.2341...], [-0.4694..., 0.5425...], [ 1.579..., 0.7674...]]) >>> y array([ 6.737..., 37.79..., -10.27..., 0.4017..., 42.22...])
Examples using sklearn.datasets.make_regression¶

Fitting an Elastic Net with a precomputed Gram Matrix and Weighted Samples
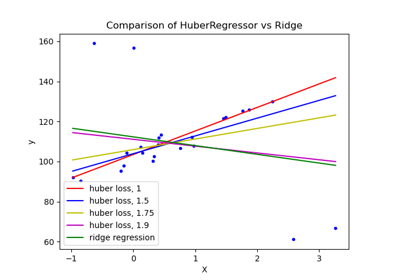
HuberRegressor vs Ridge on dataset with strong outliers
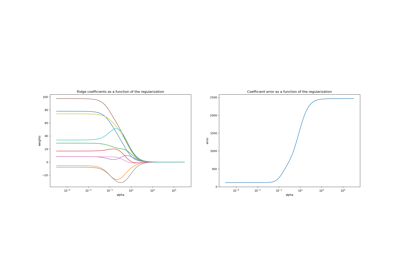
Plot Ridge coefficients as a function of the L2 regularization
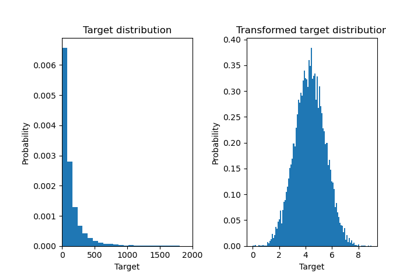
Effect of transforming the targets in regression model