Note
Click here to download the full example code or to run this example in your browser via Binder
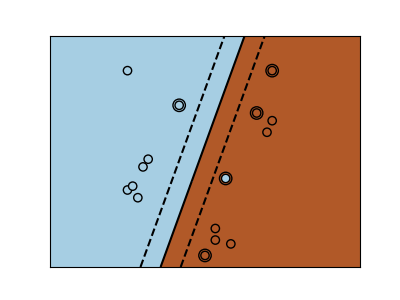
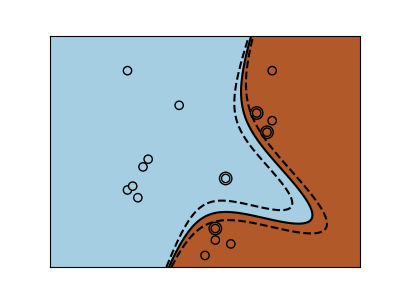
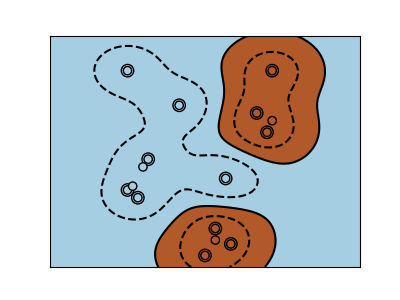
SVM-Kernels¶
Three different types of SVM-Kernels are displayed below. The polynomial and RBF are especially useful when the data-points are not linearly separable.
# Code source: Gaël Varoquaux
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
# Our dataset and targets
X = np.c_[
(0.4, -0.7),
(-1.5, -1),
(-1.4, -0.9),
(-1.3, -1.2),
(-1.1, -0.2),
(-1.2, -0.4),
(-0.5, 1.2),
(-1.5, 2.1),
(1, 1),
# --
(1.3, 0.8),
(1.2, 0.5),
(0.2, -2),
(0.5, -2.4),
(0.2, -2.3),
(0, -2.7),
(1.3, 2.1),
].T
Y = [0] * 8 + [1] * 8
# figure number
fignum = 1
# fit the model
for kernel in ("linear", "poly", "rbf"):
clf = svm.SVC(kernel=kernel, gamma=2)
clf.fit(X, Y)
# plot the line, the points, and the nearest vectors to the plane
plt.figure(fignum, figsize=(4, 3))
plt.clf()
plt.scatter(
clf.support_vectors_[:, 0],
clf.support_vectors_[:, 1],
s=80,
facecolors="none",
zorder=10,
edgecolors="k",
)
plt.scatter(X[:, 0], X[:, 1], c=Y, zorder=10, cmap=plt.cm.Paired, edgecolors="k")
plt.axis("tight")
x_min = -3
x_max = 3
y_min = -3
y_max = 3
XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()])
# Put the result into a color plot
Z = Z.reshape(XX.shape)
plt.figure(fignum, figsize=(4, 3))
plt.pcolormesh(XX, YY, Z > 0, cmap=plt.cm.Paired)
plt.contour(
XX,
YY,
Z,
colors=["k", "k", "k"],
linestyles=["--", "-", "--"],
levels=[-0.5, 0, 0.5],
)
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
fignum = fignum + 1
plt.show()
Total running time of the script: ( 0 minutes 0.196 seconds)