Lasso and Elastic Net for Sparse Signals

Estimates Lasso and Elastic-Net regression models on a manually generated sparse signal corrupted with an additive noise. Estimated coefficients are compared with the ground-truth.

Data Generation

import numpy as np
import matplotlib.pyplot as plt

from sklearn.metrics import r2_score

np.random.seed(42)

n_samples, n_features = 50, 100
X = np.random.randn(n_samples, n_features)

# Decreasing coef w. alternated signs for visualization
idx = np.arange(n_features)
coef = (-1) ** idx * np.exp(-idx / 10)
coef[10:] = 0  # sparsify coef
y = np.dot(X, coef)

# Add noise
y += 0.01 * np.random.normal(size=n_samples)

# Split data in train set and test set
n_samples = X.shape[0]
X_train, y_train = X[: n_samples // 2], y[: n_samples // 2]
X_test, y_test = X[n_samples // 2 :], y[n_samples // 2 :]

Lasso

from sklearn.linear_model import Lasso

alpha = 0.1
lasso = Lasso(alpha=alpha)

y_pred_lasso = lasso.fit(X_train, y_train).predict(X_test)
r2_score_lasso = r2_score(y_test, y_pred_lasso)
print(lasso)
print("r^2 on test data : %f" % r2_score_lasso)

Lasso(alpha=0.1)
r^2 on test data : 0.658064

ElasticNet

from sklearn.linear_model import ElasticNet

enet = ElasticNet(alpha=alpha, l1_ratio=0.7)

y_pred_enet = enet.fit(X_train, y_train).predict(X_test)
r2_score_enet = r2_score(y_test, y_pred_enet)
print(enet)
print("r^2 on test data : %f" % r2_score_enet)

ElasticNet(alpha=0.1, l1_ratio=0.7)
r^2 on test data : 0.642515

Plot

m, s, _ = plt.stem(
    np.where(enet.coef_)[0],
    enet.coef_[enet.coef_ != 0],
    markerfmt="x",
    label="Elastic net coefficients",
)
plt.setp([m, s], color="#2ca02c")
m, s, _ = plt.stem(
    np.where(lasso.coef_)[0],
    lasso.coef_[lasso.coef_ != 0],
    markerfmt="x",
    label="Lasso coefficients",
)
plt.setp([m, s], color="#ff7f0e")
plt.stem(
    np.where(coef)[0],
    coef[coef != 0],
    label="true coefficients",
    markerfmt="bx",
)

plt.legend(loc="best")
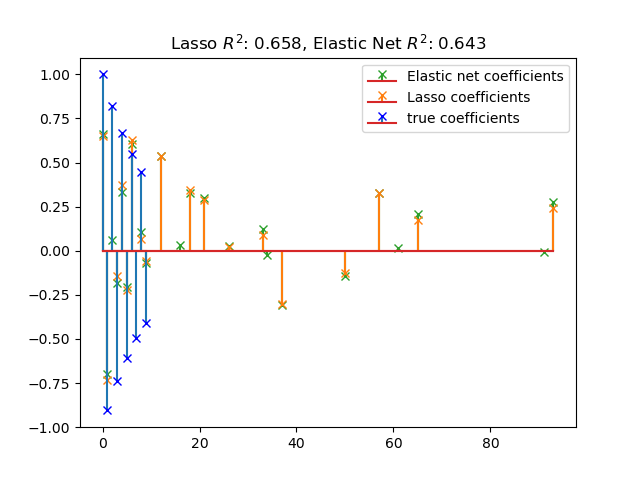
plt.title(
    "Lasso $R^2$: %.3f, Elastic Net $R^2$: %.3f" % (r2_score_lasso, r2_score_enet)
)
plt.show()