Probability Calibration curves

When performing classification one often wants to predict not only the class label, but also the associated probability. This probability gives some kind of confidence on the prediction. This example demonstrates how to visualize how well calibrated the predicted probabilities are using calibration curves, also known as reliability diagrams. Calibration of an uncalibrated classifier will also be demonstrated.

# Author: Alexandre Gramfort <alexandre.gramfort@telecom-paristech.fr>
#         Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
# License: BSD 3 clause.

Dataset

We will use a synthetic binary classification dataset with 100,000 samples and 20 features. Of the 20 features, only 2 are informative, 10 are redundant (random combinations of the informative features) and the remaining 8 are uninformative (random numbers). Of the 100,000 samples, 1,000 will be used for model fitting and the rest for testing.

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

X, y = make_classification(
    n_samples=100_000, n_features=20, n_informative=2, n_redundant=10, random_state=42
)

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.99, random_state=42
)

Calibration curves

Gaussian Naive Bayes

First, we will compare:

• LogisticRegression (used as baseline since very often, properly regularized logistic regression is well calibrated by default thanks to the use of the log-loss)

• Uncalibrated GaussianNB

• GaussianNB with isotonic and sigmoid calibration (see User Guide)

Calibration curves for all 4 conditions are plotted below, with the average predicted probability for each bin on the x-axis and the fraction of positive classes in each bin on the y-axis.

import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec

from sklearn.calibration import CalibratedClassifierCV, CalibrationDisplay
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB

lr = LogisticRegression(C=1.0)
gnb = GaussianNB()
gnb_isotonic = CalibratedClassifierCV(gnb, cv=2, method="isotonic")
gnb_sigmoid = CalibratedClassifierCV(gnb, cv=2, method="sigmoid")

clf_list = [
    (lr, "Logistic"),
    (gnb, "Naive Bayes"),
    (gnb_isotonic, "Naive Bayes + Isotonic"),
    (gnb_sigmoid, "Naive Bayes + Sigmoid"),
]

fig = plt.figure(figsize=(10, 10))
gs = GridSpec(4, 2)
colors = plt.cm.get_cmap("Dark2")

ax_calibration_curve = fig.add_subplot(gs[:2, :2])
calibration_displays = {}
for i, (clf, name) in enumerate(clf_list):
    clf.fit(X_train, y_train)
    display = CalibrationDisplay.from_estimator(
        clf,
        X_test,
        y_test,
        n_bins=10,
        name=name,
        ax=ax_calibration_curve,
        color=colors(i),
    )
    calibration_displays[name] = display

ax_calibration_curve.grid()
ax_calibration_curve.set_title("Calibration plots (Naive Bayes)")

# Add histogram
grid_positions = [(2, 0), (2, 1), (3, 0), (3, 1)]
for i, (_, name) in enumerate(clf_list):
    row, col = grid_positions[i]
    ax = fig.add_subplot(gs[row, col])

    ax.hist(
        calibration_displays[name].y_prob,
        range=(0, 1),
        bins=10,
        label=name,
        color=colors(i),
    )
    ax.set(title=name, xlabel="Mean predicted probability", ylabel="Count")

plt.tight_layout()
plt.show()

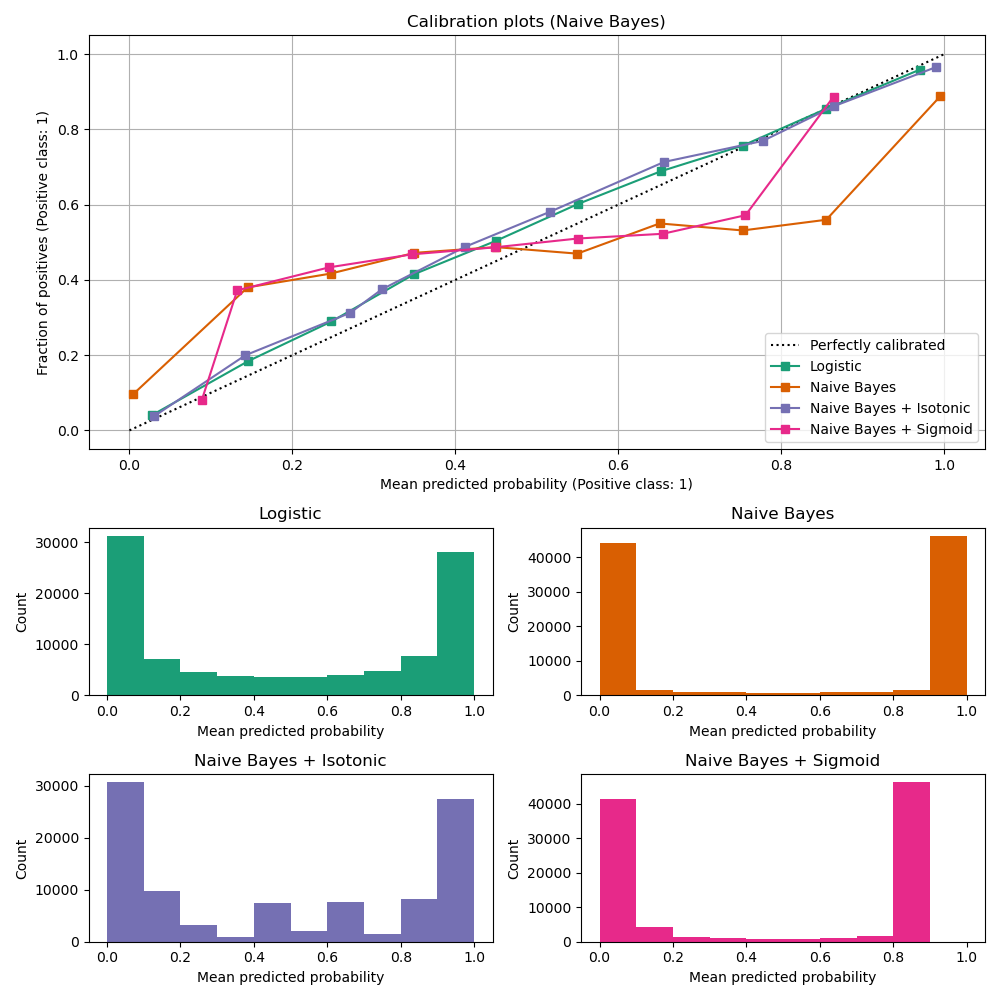
Uncalibrated GaussianNB is poorly calibrated because of the redundant features which violate the assumption of feature-independence and result in an overly confident classifier, which is indicated by the typical transposed-sigmoid curve. Calibration of the probabilities of GaussianNB with Isotonic regression can fix this issue as can be seen from the nearly diagonal calibration curve. :ref:sigmoid regression <sigmoid_regressor> also improves calibration slightly, albeit not as strongly as the non-parametric isotonic regression. This can be attributed to the fact that we have plenty of calibration data such that the greater flexibility of the non-parametric model can be exploited.

Below we will make a quantitative analysis considering several classification metrics: Brier score loss, Log loss, precision, recall, F1 score and ROC AUC.

from collections import defaultdict

import pandas as pd

from sklearn.metrics import (
    precision_score,
    recall_score,
    f1_score,
    brier_score_loss,
    log_loss,
    roc_auc_score,
)

scores = defaultdict(list)
for i, (clf, name) in enumerate(clf_list):
    clf.fit(X_train, y_train)
    y_prob = clf.predict_proba(X_test)
    y_pred = clf.predict(X_test)
    scores["Classifier"].append(name)

    for metric in [brier_score_loss, log_loss]:
        score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
        scores[score_name].append(metric(y_test, y_prob[:, 1]))

    for metric in [precision_score, recall_score, f1_score, roc_auc_score]:
        score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
        scores[score_name].append(metric(y_test, y_pred))

    score_df = pd.DataFrame(scores).set_index("Classifier")
    score_df.round(decimals=3)

score_df

	Brier loss	Log loss	Precision	Recall	F1	Roc auc
Classifier
Logistic	0.098921	0.323178	0.872009	0.851408	0.861586	0.863157
Naive Bayes	0.117608	0.782247	0.857400	0.875941	0.866571	0.865055
Naive Bayes + Isotonic	0.098332	0.368412	0.883065	0.836224	0.859007	0.862690
Naive Bayes + Sigmoid	0.108880	0.368896	0.861106	0.871277	0.866161	0.865300

Notice that although calibration improves the Brier score loss (a metric composed of calibration term and refinement term) and Log loss, it does not significantly alter the prediction accuracy measures (precision, recall and F1 score). This is because calibration should not significantly change prediction probabilities at the location of the decision threshold (at x = 0.5 on the graph). Calibration should however, make the predicted probabilities more accurate and thus more useful for making allocation decisions under uncertainty. Further, ROC AUC, should not change at all because calibration is a monotonic transformation. Indeed, no rank metrics are affected by calibration.

Linear support vector classifier

Next, we will compare:

• LogisticRegression (baseline)

• Uncalibrated LinearSVC. Since SVC does not output probabilities by default, we naively scale the output of the decision_function into [0, 1] by applying min-max scaling.

• LinearSVC with isotonic and sigmoid calibration (see User Guide)

import numpy as np

from sklearn.svm import LinearSVC


class NaivelyCalibratedLinearSVC(LinearSVC):
    """LinearSVC with `predict_proba` method that naively scales
    `decision_function` output for binary classification."""

    def fit(self, X, y):
        super().fit(X, y)
        df = self.decision_function(X)
        self.df_min_ = df.min()
        self.df_max_ = df.max()

    def predict_proba(self, X):
        """Min-max scale output of `decision_function` to [0, 1]."""
        df = self.decision_function(X)
        calibrated_df = (df - self.df_min_) / (self.df_max_ - self.df_min_)
        proba_pos_class = np.clip(calibrated_df, 0, 1)
        proba_neg_class = 1 - proba_pos_class
        proba = np.c_[proba_neg_class, proba_pos_class]
        return proba

lr = LogisticRegression(C=1.0)
svc = NaivelyCalibratedLinearSVC(max_iter=10_000)
svc_isotonic = CalibratedClassifierCV(svc, cv=2, method="isotonic")
svc_sigmoid = CalibratedClassifierCV(svc, cv=2, method="sigmoid")

clf_list = [
    (lr, "Logistic"),
    (svc, "SVC"),
    (svc_isotonic, "SVC + Isotonic"),
    (svc_sigmoid, "SVC + Sigmoid"),
]

fig = plt.figure(figsize=(10, 10))
gs = GridSpec(4, 2)

ax_calibration_curve = fig.add_subplot(gs[:2, :2])
calibration_displays = {}
for i, (clf, name) in enumerate(clf_list):
    clf.fit(X_train, y_train)
    display = CalibrationDisplay.from_estimator(
        clf,
        X_test,
        y_test,
        n_bins=10,
        name=name,
        ax=ax_calibration_curve,
        color=colors(i),
    )
    calibration_displays[name] = display

ax_calibration_curve.grid()
ax_calibration_curve.set_title("Calibration plots (SVC)")

# Add histogram
grid_positions = [(2, 0), (2, 1), (3, 0), (3, 1)]
for i, (_, name) in enumerate(clf_list):
    row, col = grid_positions[i]
    ax = fig.add_subplot(gs[row, col])

    ax.hist(
        calibration_displays[name].y_prob,
        range=(0, 1),
        bins=10,
        label=name,
        color=colors(i),
    )
    ax.set(title=name, xlabel="Mean predicted probability", ylabel="Count")

plt.tight_layout()
plt.show()

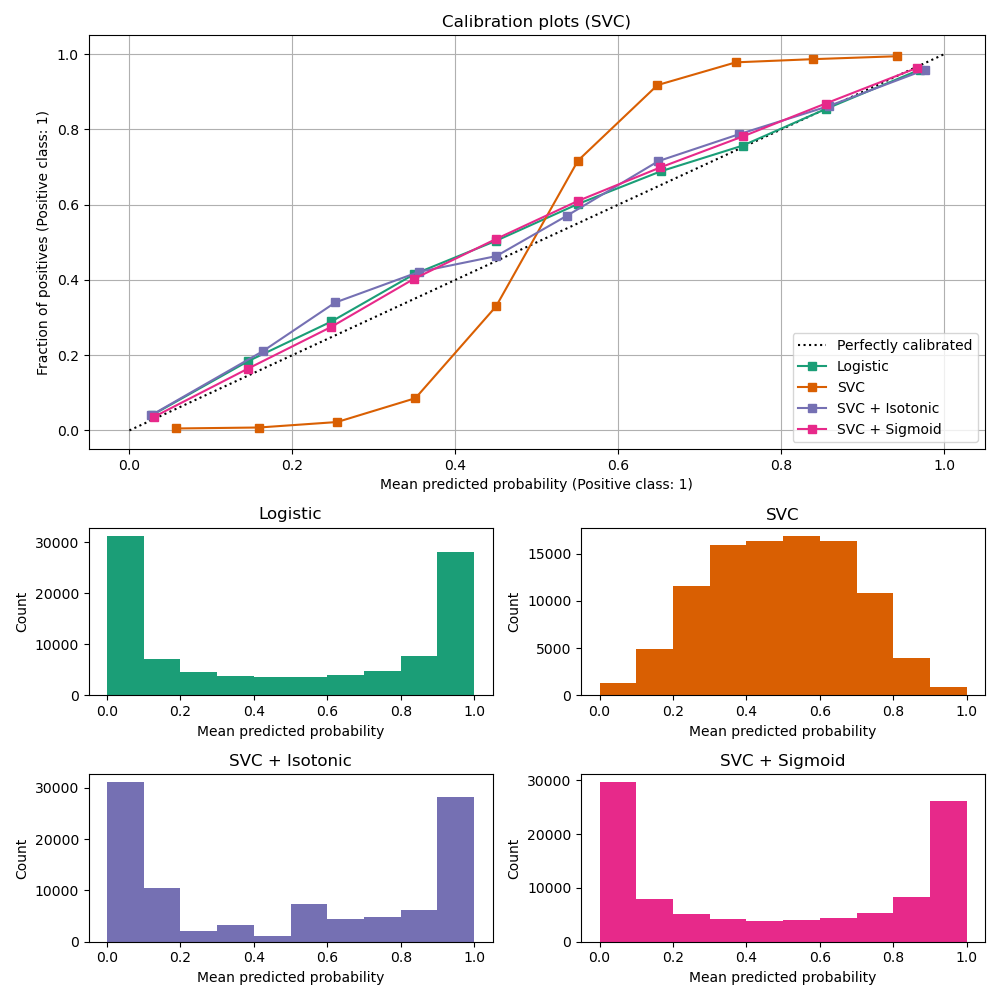
LinearSVC shows the opposite behavior to GaussianNB; the calibration curve has a sigmoid shape, which is typical for an under-confident classifier. In the case of LinearSVC, this is caused by the margin property of the hinge loss, which focuses on samples that are close to the decision boundary (support vectors). Samples that are far away from the decision boundary do not impact the hinge loss. It thus makes sense that LinearSVC does not try to separate samples in the high confidence region regions. This leads to flatter calibration curves near 0 and 1 and is empirically shown with a variety of datasets in Niculescu-Mizil & Caruana [1].

Both kinds of calibration (sigmoid and isotonic) can fix this issue and yield similar results.

As before, we show the Brier score loss, Log loss, precision, recall, F1 score and ROC AUC.

scores = defaultdict(list)
for i, (clf, name) in enumerate(clf_list):
    clf.fit(X_train, y_train)
    y_prob = clf.predict_proba(X_test)
    y_pred = clf.predict(X_test)
    scores["Classifier"].append(name)

    for metric in [brier_score_loss, log_loss]:
        score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
        scores[score_name].append(metric(y_test, y_prob[:, 1]))

    for metric in [precision_score, recall_score, f1_score, roc_auc_score]:
        score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
        scores[score_name].append(metric(y_test, y_pred))

    score_df = pd.DataFrame(scores).set_index("Classifier")
    score_df.round(decimals=3)

score_df

	Brier loss	Log loss	Precision	Recall	F1	Roc auc
Classifier
Logistic	0.098921	0.323178	0.872009	0.851408	0.861586	0.863157
SVC	0.144944	0.465647	0.872201	0.851772	0.861865	0.863420
SVC + Isotonic	0.099827	0.374535	0.853032	0.878041	0.865356	0.863306
SVC + Sigmoid	0.098760	0.321306	0.873703	0.848723	0.861032	0.862957

As with GaussianNB above, calibration improves both Brier score loss and Log loss but does not alter the prediction accuracy measures (precision, recall and F1 score) much.

Summary

Parametric sigmoid calibration can deal with situations where the calibration curve of the base classifier is sigmoid (e.g., for LinearSVC) but not where it is transposed-sigmoid (e.g., GaussianNB). Non-parametric isotonic calibration can deal with both situations but may require more data to produce good results.

References

[1]

Predicting Good Probabilities with Supervised Learning, A. Niculescu-Mizil & R. Caruana, ICML 2005