sklearn.linear_model.lasso_path

sklearn.linear_model.lasso_path(X, y, *, eps=0.001, n_alphas=100, alphas=None, precompute='auto', Xy=None, copy_X=True, coef_init=None, verbose=False, return_n_iter=False, positive=False, **params)

Compute Lasso path with coordinate descent.

The Lasso optimization function varies for mono and multi-outputs.

For mono-output tasks it is:

(1 / (2 * n_samples)) * ||y - Xw||^2_2 + alpha * ||w||_1

For multi-output tasks it is:

(1 / (2 * n_samples)) * ||Y - XW||^2_Fro + alpha * ||W||_21

Where:

||W||_21 = \sum_i \sqrt{\sum_j w_{ij}^2}

i.e. the sum of norm of each row.

Read more in the User Guide.

Parameters

X{array-like, sparse matrix} of shape (n_samples, n_features)

Training data. Pass directly as Fortran-contiguous data to avoid unnecessary memory duplication. If y is mono-output then X can be sparse.

y{array-like, sparse matrix} of shape (n_samples,) or (n_samples, n_targets)

Target values.

epsfloat, default=1e-3

Length of the path. eps=1e-3 means that alpha_min / alpha_max = 1e-3.

n_alphasint, default=100

Number of alphas along the regularization path.

alphasndarray, default=None

List of alphas where to compute the models. If None alphas are set automatically.

precompute‘auto’, bool or array-like of shape (n_features, n_features), default=’auto’

Whether to use a precomputed Gram matrix to speed up calculations. If set to 'auto' let us decide. The Gram matrix can also be passed as argument.

Xyarray-like of shape (n_features,) or (n_features, n_targets), default=None

Xy = np.dot(X.T, y) that can be precomputed. It is useful only when the Gram matrix is precomputed.

copy_Xbool, default=True

If True, X will be copied; else, it may be overwritten.

coef_initndarray of shape (n_features, ), default=None

The initial values of the coefficients.

verbosebool or int, default=False

Amount of verbosity.

return_n_iterbool, default=False

Whether to return the number of iterations or not.

positivebool, default=False

If set to True, forces coefficients to be positive. (Only allowed when y.ndim == 1).

**paramskwargs

Keyword arguments passed to the coordinate descent solver.

Returns

alphasndarray of shape (n_alphas,)

The alphas along the path where models are computed.

coefsndarray of shape (n_features, n_alphas) or (n_targets, n_features, n_alphas)

Coefficients along the path.

dual_gapsndarray of shape (n_alphas,)

The dual gaps at the end of the optimization for each alpha.

n_iterslist of int

The number of iterations taken by the coordinate descent optimizer to reach the specified tolerance for each alpha.

See also

lars_path

Compute Least Angle Regression or Lasso path using LARS algorithm.

Lasso

The Lasso is a linear model that estimates sparse coefficients.

LassoLars

Lasso model fit with Least Angle Regression a.k.a. Lars.

LassoCV

Lasso linear model with iterative fitting along a regularization path.

LassoLarsCV

Cross-validated Lasso using the LARS algorithm.

sklearn.decomposition.sparse_encode

Estimator that can be used to transform signals into sparse linear combination of atoms from a fixed.

Notes

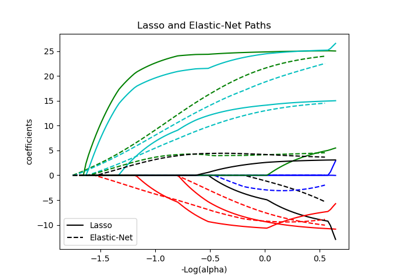
For an example, see examples/linear_model/plot_lasso_coordinate_descent_path.py.

To avoid unnecessary memory duplication the X argument of the fit method should be directly passed as a Fortran-contiguous numpy array.

Note that in certain cases, the Lars solver may be significantly faster to implement this functionality. In particular, linear interpolation can be used to retrieve model coefficients between the values output by lars_path

Examples

Comparing lasso_path and lars_path with interpolation:

>>> import numpy as np
>>> from sklearn.linear_model import lasso_path
>>> X = np.array([[1, 2, 3.1], [2.3, 5.4, 4.3]]).T
>>> y = np.array([1, 2, 3.1])
>>> # Use lasso_path to compute a coefficient path
>>> _, coef_path, _ = lasso_path(X, y, alphas=[5., 1., .5])
>>> print(coef_path)
[[0.         0.         0.46874778]
 [0.2159048  0.4425765  0.23689075]]

>>> # Now use lars_path and 1D linear interpolation to compute the
>>> # same path
>>> from sklearn.linear_model import lars_path
>>> alphas, active, coef_path_lars = lars_path(X, y, method='lasso')
>>> from scipy import interpolate
>>> coef_path_continuous = interpolate.interp1d(alphas[::-1],
...                                             coef_path_lars[:, ::-1])
>>> print(coef_path_continuous([5., 1., .5]))
[[0.         0.         0.46915237]
 [0.2159048  0.4425765  0.23668876]]

Examples using sklearn.linear_model.lasso_path

Lasso and Elastic Net