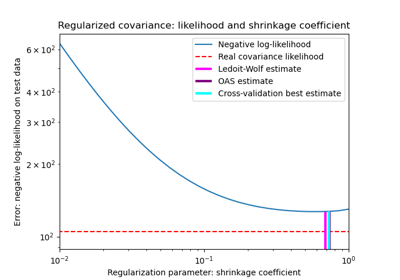
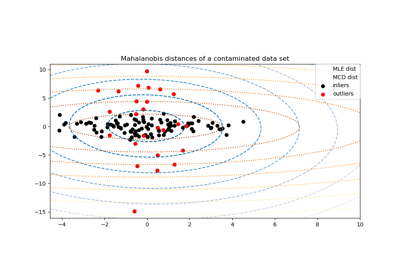
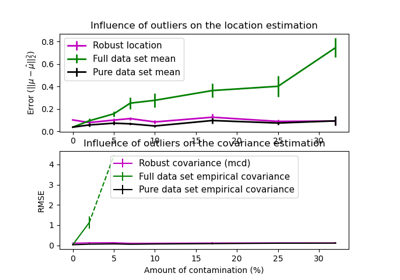
sklearn.covariance.EmpiricalCovariance

class sklearn.covariance.EmpiricalCovariance(*, store_precision=True, assume_centered=False)

Maximum likelihood covariance estimator.

Read more in the User Guide.

Parameters

store_precisionbool, default=True

Specifies if the estimated precision is stored.

assume_centeredbool, default=False

If True, data are not centered before computation. Useful when working with data whose mean is almost, but not exactly zero. If False (default), data are centered before computation.

Attributes

location_ndarray of shape (n_features,)

Estimated location, i.e. the estimated mean.

covariance_ndarray of shape (n_features, n_features)

Estimated covariance matrix

precision_ndarray of shape (n_features, n_features)

Estimated pseudo-inverse matrix. (stored only if store_precision is True)

n_features_in_int

Number of features seen during fit.

New in version 0.24.

feature_names_in_ndarray of shape (n_features_in_,)

Names of features seen during fit. Defined only when X has feature names that are all strings.

New in version 1.0.

See also

EllipticEnvelope

An object for detecting outliers in a Gaussian distributed dataset.

GraphicalLasso

Sparse inverse covariance estimation with an l1-penalized estimator.

LedoitWolf

LedoitWolf Estimator.

MinCovDet

Minimum Covariance Determinant (robust estimator of covariance).

OAS

Oracle Approximating Shrinkage Estimator.

ShrunkCovariance

Covariance estimator with shrinkage.

Examples

>>> import numpy as np
>>> from sklearn.covariance import EmpiricalCovariance
>>> from sklearn.datasets import make_gaussian_quantiles
>>> real_cov = np.array([[.8, .3],
...                      [.3, .4]])
>>> rng = np.random.RandomState(0)
>>> X = rng.multivariate_normal(mean=[0, 0],
...                             cov=real_cov,
...                             size=500)
>>> cov = EmpiricalCovariance().fit(X)
>>> cov.covariance_
array([[0.7569..., 0.2818...],
       [0.2818..., 0.3928...]])
>>> cov.location_
array([0.0622..., 0.0193...])

Methods

error_norm(comp_cov[, norm, scaling, squared])	Compute the Mean Squared Error between two covariance estimators.
fit(X[, y])	Fit the maximum liklihood covariance estimator to X.
get_params([deep])	Get parameters for this estimator.
get_precision()	Getter for the precision matrix.
mahalanobis(X)	Compute the squared Mahalanobis distances of given observations.
score(X_test[, y])	Compute the log-likelihood of X_test under the estimated Gaussian model.
set_params(**params)	Set the parameters of this estimator.

error_norm(comp_cov, norm='frobenius', scaling=True, squared=True)

Compute the Mean Squared Error between two covariance estimators.

Parameters

comp_covarray-like of shape (n_features, n_features)

The covariance to compare with.

norm{“frobenius”, “spectral”}, default=”frobenius”

The type of norm used to compute the error. Available error types: - ‘frobenius’ (default): sqrt(tr(A^t.A)) - ‘spectral’: sqrt(max(eigenvalues(A^t.A)) where A is the error (comp_cov - self.covariance_).

scalingbool, default=True

If True (default), the squared error norm is divided by n_features. If False, the squared error norm is not rescaled.

squaredbool, default=True

Whether to compute the squared error norm or the error norm. If True (default), the squared error norm is returned. If False, the error norm is returned.

Returns

resultfloat

The Mean Squared Error (in the sense of the Frobenius norm) between self and comp_cov covariance estimators.

fit(X, y=None)

Fit the maximum liklihood covariance estimator to X.

Parameters

Xarray-like of shape (n_samples, n_features)

Training data, where n_samples is the number of samples and n_features is the number of features.

yIgnored

Not used, present for API consistency by convention.

Returns

selfobject

Returns the instance itself.

get_params(deep=True)

Get parameters for this estimator.

Parameters

deepbool, default=True

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns

paramsdict

Parameter names mapped to their values.

get_precision()

Getter for the precision matrix.

Returns

precision_array-like of shape (n_features, n_features)

The precision matrix associated to the current covariance object.

mahalanobis(X)

Compute the squared Mahalanobis distances of given observations.

Parameters

Xarray-like of shape (n_samples, n_features)

The observations, the Mahalanobis distances of the which we compute. Observations are assumed to be drawn from the same distribution than the data used in fit.

Returns

distndarray of shape (n_samples,)

Squared Mahalanobis distances of the observations.

score(X_test, y=None)

Compute the log-likelihood of X_test under the estimated Gaussian model.

The Gaussian model is defined by its mean and covariance matrix which are represented respectively by self.location_ and self.covariance_.

Parameters

X_testarray-like of shape (n_samples, n_features)

Test data of which we compute the likelihood, where n_samples is the number of samples and n_features is the number of features. X_test is assumed to be drawn from the same distribution than the data used in fit (including centering).

yIgnored

Not used, present for API consistency by convention.

Returns

resfloat

The log-likelihood of X_test with self.location_ and self.covariance_ as estimators of the Gaussian model mean and covariance matrix respectively.

set_params(**params)

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters

**paramsdict

Estimator parameters.

Returns

selfestimator instance

Estimator instance.

Examples using sklearn.covariance.EmpiricalCovariance

Shrinkage covariance estimation: LedoitWolf vs OAS and max-likelihood

Robust covariance estimation and Mahalanobis distances relevance

Robust vs Empirical covariance estimate