This is documentation for an old release of Scikit-learn (version 0.23). Try the latest stable release (version 1.6) or development (unstable) versions.

4.1. Partial dependence plots¶

Partial dependence plots (PDP) show the dependence between the target response 1 and a set of ‘target’ features, marginalizing over the values of all other features (the ‘complement’ features). Intuitively, we can interpret the partial dependence as the expected target response as a function of the ‘target’ features.

Due to the limits of human perception the size of the target feature set must be small (usually, one or two) thus the target features are usually chosen among the most important features.

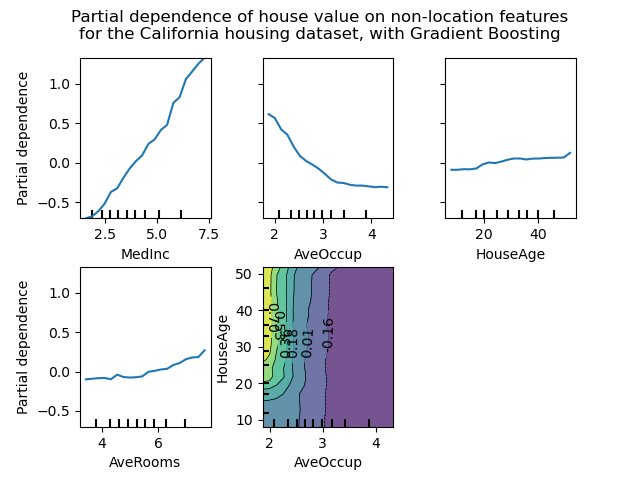
The figure below shows four one-way and one two-way partial dependence plots for the California housing dataset, with a GradientBoostingRegressor:

../_images/sphx_glr_plot_partial_dependence_0021.png

One-way PDPs tell us about the interaction between the target response and the target feature (e.g. linear, non-linear). The upper left plot in the above figure shows the effect of the median income in a district on the median house price; we can clearly see a linear relationship among them. Note that PDPs assume that the target features are independent from the complement features, and this assumption is often violated in practice.

PDPs with two target features show the interactions among the two features. For example, the two-variable PDP in the above figure shows the dependence of median house price on joint values of house age and average occupants per household. We can clearly see an interaction between the two features: for an average occupancy greater than two, the house price is nearly independent of the house age, whereas for values less than 2 there is a strong dependence on age.

The sklearn.inspection module provides a convenience function plot_partial_dependence to create one-way and two-way partial dependence plots. In the below example we show how to create a grid of partial dependence plots: two one-way PDPs for the features 0 and 1 and a two-way PDP between the two features:

>>>>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> from sklearn.inspection import plot_partial_dependence

>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
...     max_depth=1, random_state=0).fit(X, y)
>>> features = [0, 1, (0, 1)]
>>> plot_partial_dependence(clf, X, features) 

You can access the newly created figure and Axes objects using plt.gcf() and plt.gca().

For multi-class classification, you need to set the class label for which the PDPs should be created via the target argument:

>>>>>> from sklearn.datasets import load_iris
>>> iris = load_iris()
>>> mc_clf = GradientBoostingClassifier(n_estimators=10,
...     max_depth=1).fit(iris.data, iris.target)
>>> features = [3, 2, (3, 2)]
>>> plot_partial_dependence(mc_clf, X, features, target=0) 

The same parameter target is used to specify the target in multi-output regression settings.

If you need the raw values of the partial dependence function rather than the plots, you can use the sklearn.inspection.partial_dependence function:

>>>>>> from sklearn.inspection import partial_dependence

>>> pdp, axes = partial_dependence(clf, X, [0])
>>> pdp
array([[ 2.466...,  2.466..., ...
>>> axes
[array([-1.624..., -1.592..., ...

The values at which the partial dependence should be evaluated are directly generated from X. For 2-way partial dependence, a 2D-grid of values is generated. The values field returned by sklearn.inspection.partial_dependence gives the actual values used in the grid for each target feature. They also correspond to the axis of the plots.

4.1.1. Mathematical Definition¶

Let $X_{S}$ be the set of target features (i.e. the features parameter) and let $X_{C}$ be its complement.

The partial dependence of the response $f$ at a point $x_{S}$ is defined as:

\begin{aligned} p d_{X_{S}} (x_{S}) & \overset{d e f}{=} E_{X_{C}} [f (x_{S}, X_{C})] \\ = \int f (x_{S}, x_{C}) p (x_{C}) d x_{C}, \end{aligned}

where $f (x_{S}, x_{C})$ is the response function (predict, predict_proba or decision_function) for a given sample whose values are defined by $x_{S}$ for the features in $X_{S}$ , and by $x_{C}$ for the features in $X_{C}$ . Note that $x_{S}$ and $x_{C}$ may be tuples.

Computing this integral for various values of $x_{S}$ produces a plot as above.

4.1.2. Computation methods¶

There are two main methods to approximate the integral above, namely the ‘brute’ and ‘recursion’ methods. The method parameter controls which method to use.

The ‘brute’ method is a generic method that works with any estimator. It approximates the above integral by computing an average over the data X:

p d_{X_{S}} (x_{S}) \approx \frac{1}{n_{samples}} \sum_{i = 1}^{n} f (x_{S}, x_{C}^{(i)}),

where $x_{C}^{(i)}$ is the value of the i-th sample for the features in $X_{C}$ . For each value of $x_{S}$ , this method requires a full pass over the dataset X which is computationally intensive.

The ‘recursion’ method is faster than the ‘brute’ method, but it is only supported by some tree-based estimators. It is computed as follows. For a given point $x_{S}$ , a weighted tree traversal is performed: if a split node involves a ‘target’ feature, the corresponding left or right branch is followed; otherwise both branches are followed, each branch being weighted by the fraction of training samples that entered that branch. Finally, the partial dependence is given by a weighted average of all the visited leaves values.

With the ‘brute’ method, the parameter X is used both for generating the grid of values $x_{S}$ and the complement feature values $x_{C}$ . However with the ‘recursion’ method, X is only used for the grid values: implicitly, the $x_{C}$ values are those of the training data.

By default, the ‘recursion’ method is used on tree-based estimators that support it, and ‘brute’ is used for the rest.

Note

While both methods should be close in general, they might differ in some specific settings. The ‘brute’ method assumes the existence of the data points $(x_{S}, x_{C}^{(i)})$ . When the features are correlated, such artificial samples may have a very low probability mass. The ‘brute’ and ‘recursion’ methods will likely disagree regarding the value of the partial dependence, because they will treat these unlikely samples differently. Remember, however, that the primary assumption for interpreting PDPs is that the features should be independent.

Footnotes

1: For classification, the target response may be the probability of a class (the positive class for binary classification), or the decision function.

Examples:

Partial Dependence Plots

References

T. Hastie, R. Tibshirani and J. Friedman, The Elements of Statistical Learning, Second Edition, Section 10.13.2, Springer, 2009.

C. Molnar, Interpretable Machine Learning, Section 5.1, 2019.