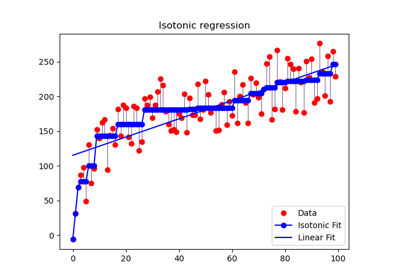
sklearn.isotonic.IsotonicRegression

class sklearn.isotonic.IsotonicRegression(*, y_min=None, y_max=None, increasing=True, out_of_bounds='nan')[source]

Isotonic regression model.

Read more in the User Guide.

New in version 0.13.

Parameters
y_minfloat, default=None

Lower bound on the lowest predicted value (the minimum value may still be higher). If not set, defaults to -inf.

y_maxfloat, default=None

Upper bound on the highest predicted value (the maximum may still be lower). If not set, defaults to +inf.

increasingbool or ‘auto’, default=True

Determines whether the predictions should be constrained to increase or decrease with X. ‘auto’ will decide based on the Spearman correlation estimate’s sign.

out_of_boundsstr, default=”nan”

The out_of_bounds parameter handles how X values outside of the training domain are handled. When set to “nan”, predictions will be NaN. When set to “clip”, predictions will be set to the value corresponding to the nearest train interval endpoint. When set to “raise” a ValueError is raised.

Attributes
X_min_float

Minimum value of input array X_ for left bound.

X_max_float

Maximum value of input array X_ for right bound.

f_function

The stepwise interpolating function that covers the input domain X.

increasing_bool

Inferred value for increasing.

Notes

Ties are broken using the secondary method from Leeuw, 1977.

References

Isotonic Median Regression: A Linear Programming Approach Nilotpal Chakravarti Mathematics of Operations Research Vol. 14, No. 2 (May, 1989), pp. 303-308

Isotone Optimization in R : Pool-Adjacent-Violators Algorithm (PAVA) and Active Set Methods Leeuw, Hornik, Mair Journal of Statistical Software 2009

Correctness of Kruskal’s algorithms for monotone regression with ties Leeuw, Psychometrica, 1977

Examples

>>> from sklearn.datasets import make_regression
>>> from sklearn.isotonic import IsotonicRegression
>>> X, y = make_regression(n_samples=10, n_features=1, random_state=41)
>>> iso_reg = IsotonicRegression().fit(X.flatten(), y)
>>> iso_reg.predict([.1, .2])
array([1.8628..., 3.7256...])

Methods

fit(X, y[, sample_weight])

Fit the model using X, y as training data.

fit_transform(X[, y])

Fit to data, then transform it.

get_params([deep])

Get parameters for this estimator.

predict(T)

Predict new data by linear interpolation.

score(X, y[, sample_weight])

Return the coefficient of determination R^2 of the prediction.

set_params(**params)

Set the parameters of this estimator.

transform(T)

Transform new data by linear interpolation
__init__(*, y_min=None, y_max=None, increasing=True, out_of_bounds='nan')[source]

Initialize self. See help(type(self)) for accurate signature.

fit(X, y, sample_weight=None)[source]

Fit the model using X, y as training data.

Parameters
Xarray-like of shape (n_samples,)

Training data.

yarray-like of shape (n_samples,)

Training target.

sample_weightarray-like of shape (n_samples,), default=None

Weights. If set to None, all weights will be set to 1 (equal weights).

Returns
selfobject

Returns an instance of self.

Notes

X is stored for future use, as transform needs X to interpolate new input data.

fit_transform(X, y=None, **fit_params)[source]

Fit to data, then transform it.

Fits transformer to X and y with optional parameters fit_params and returns a transformed version of X.

Parameters
X{array-like, sparse matrix, dataframe} of shape (n_samples, n_features)
yndarray of shape (n_samples,), default=None

Target values.

**fit_paramsdict

Additional fit parameters.

Returns
X_newndarray array of shape (n_samples, n_features_new)

Transformed array.

get_params(deep=True)[source]

Get parameters for this estimator.

Parameters
deepbool, default=True

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns
paramsmapping of string to any

Parameter names mapped to their values.

predict(T)[source]

Predict new data by linear interpolation.

Parameters
Tarray-like of shape (n_samples,)

Data to transform.

Returns
y_predndarray of shape (n_samples,)

Transformed data.

score(X, y, sample_weight=None)[source]

Return the coefficient of determination R^2 of the prediction.

The coefficient R^2 is defined as (1 - u/v), where u is the residual sum of squares ((y_true - y_pred) ** 2).sum() and v is the total sum of squares ((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a R^2 score of 0.0.

Parameters
Xarray-like of shape (n_samples, n_features)

Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead, shape = (n_samples, n_samples_fitted), where n_samples_fitted is the number of samples used in the fitting for the estimator.

yarray-like of shape (n_samples,) or (n_samples, n_outputs)

True values for X.

sample_weightarray-like of shape (n_samples,), default=None

Sample weights.

Returns
scorefloat

R^2 of self.predict(X) wrt. y.

Notes

The R2 score used when calling score on a regressor uses multioutput='uniform_average' from version 0.23 to keep consistent with default value of r2_score. This influences the score method of all the multioutput regressors (except for MultiOutputRegressor).

set_params(**params)[source]

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as pipelines). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters
**paramsdict

Estimator parameters.

Returns
selfobject

Estimator instance.

transform(T)[source]

Transform new data by linear interpolation

Parameters
Tarray-like of shape (n_samples,)

Data to transform.

Returns
y_predndarray of shape (n_samples,)

The transformed data

Examples using sklearn.isotonic.IsotonicRegression