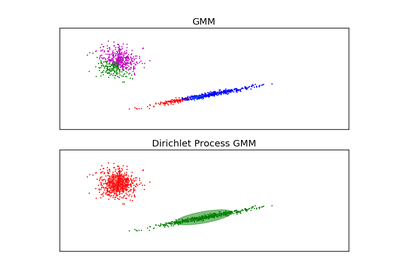
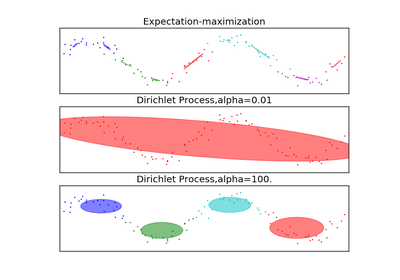
sklearn.mixture.DPGMM

class sklearn.mixture.DPGMM(n_components=1, covariance_type='diag', alpha=1.0, random_state=None, thresh=None, tol=0.001, verbose=0, min_covar=None, n_iter=10, params='wmc', init_params='wmc')

Variational Inference for the Infinite Gaussian Mixture Model.

DPGMM stands for Dirichlet Process Gaussian Mixture Model, and it is an infinite mixture model with the Dirichlet Process as a prior distribution on the number of clusters. In practice the approximate inference algorithm uses a truncated distribution with a fixed maximum number of components, but almost always the number of components actually used depends on the data.

Stick-breaking Representation of a Gaussian mixture model probability distribution. This class allows for easy and efficient inference of an approximate posterior distribution over the parameters of a Gaussian mixture model with a variable number of components (smaller than the truncation parameter n_components).

Initialization is with normally-distributed means and identity covariance, for proper convergence.

Read more in the User Guide.

Parameters:

n_components: int, default 1 :

Number of mixture components.

covariance_type: string, default ‘diag’ :

String describing the type of covariance parameters to use. Must be one of ‘spherical’, ‘tied’, ‘diag’, ‘full’.

alpha: float, default 1 :

Real number representing the concentration parameter of the dirichlet process. Intuitively, the Dirichlet Process is as likely to start a new cluster for a point as it is to add that point to a cluster with alpha elements. A higher alpha means more clusters, as the expected number of clusters is alpha*log(N).

tol : float, default 1e-3

Convergence threshold.

n_iter : int, default 10

Maximum number of iterations to perform before convergence.

params : string, default ‘wmc’

Controls which parameters are updated in the training process. Can contain any combination of ‘w’ for weights, ‘m’ for means, and ‘c’ for covars.

init_params : string, default ‘wmc’

Controls which parameters are updated in the initialization process. Can contain any combination of ‘w’ for weights, ‘m’ for means, and ‘c’ for covars. Defaults to ‘wmc’.

verbose : int, default 0

Controls output verbosity.

Attributes:

covariance_type : string

String describing the type of covariance parameters used by the DP-GMM. Must be one of ‘spherical’, ‘tied’, ‘diag’, ‘full’.

n_components : int

Number of mixture components.

weights_ : array, shape (n_components,)

Mixing weights for each mixture component.

means_ : array, shape (n_components, n_features)

Mean parameters for each mixture component.

precs_ : array

Precision (inverse covariance) parameters for each mixture component. The shape depends on covariance_type:

(`n_components`, 'n_features')                if 'spherical',
(`n_features`, `n_features`)                  if 'tied',
(`n_components`, `n_features`)                if 'diag',
(`n_components`, `n_features`, `n_features`)  if 'full'

converged_ : bool

True when convergence was reached in fit(), False otherwise.

See also

GMM

Finite Gaussian mixture model fit with EM

VBGMM

Finite Gaussian mixture model fit with a variational algorithm, better for situations where there might be too little data to get a good estimate of the covariance matrix.

Methods

aic(X)	Akaike information criterion for the current model fit
bic(X)	Bayesian information criterion for the current model fit
fit(X[, y])	Estimate model parameters with the EM algorithm.
fit_predict(X[, y])	Fit and then predict labels for data.
get_params([deep])	Get parameters for this estimator.
lower_bound(X, z)	returns a lower bound on model evidence based on X and membership
predict(X)	Predict label for data.
predict_proba(X)	Predict posterior probability of data under each Gaussian in the model.
sample([n_samples, random_state])	Generate random samples from the model.
score(X[, y])	Compute the log probability under the model.
score_samples(X)	Return the likelihood of the data under the model.
set_params(**params)	Set the parameters of this estimator.

__init__(n_components=1, covariance_type='diag', alpha=1.0, random_state=None, thresh=None, tol=0.001, verbose=0, min_covar=None, n_iter=10, params='wmc', init_params='wmc')

aic(X)

Akaike information criterion for the current model fit and the proposed data

Parameters:X : array of shape(n_samples, n_dimensions) Returns:aic: float (the lower the better) :

bic(X)

Bayesian information criterion for the current model fit and the proposed data

Parameters:X : array of shape(n_samples, n_dimensions) Returns:bic: float (the lower the better) :

fit(X, y=None)

Estimate model parameters with the EM algorithm.

A initialization step is performed before entering the expectation-maximization (EM) algorithm. If you want to avoid this step, set the keyword argument init_params to the empty string ‘’ when creating the GMM object. Likewise, if you would like just to do an initialization, set n_iter=0.

Parameters:

X : array_like, shape (n, n_features)

List of n_features-dimensional data points. Each row corresponds to a single data point.

Returns:

self :

fit_predict(X, y=None)

Fit and then predict labels for data.

Warning: due to the final maximization step in the EM algorithm, with low iterations the prediction may not be 100% accurate

New in version 0.17: fit_predict method in Gaussian Mixture Model.

Parameters:X : array-like, shape = [n_samples, n_features] Returns:C : array, shape = (n_samples,) component memberships

get_params(deep=True)

Get parameters for this estimator.

Parameters:

deep: boolean, optional :

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

params : mapping of string to any

Parameter names mapped to their values.

lower_bound(X, z)

returns a lower bound on model evidence based on X and membership

predict(X)

Predict label for data.

Parameters:X : array-like, shape = [n_samples, n_features] Returns:C : array, shape = (n_samples,) component memberships

predict_proba(X)

Predict posterior probability of data under each Gaussian in the model.

Parameters:

X : array-like, shape = [n_samples, n_features]

Returns:

responsibilities : array-like, shape = (n_samples, n_components)

Returns the probability of the sample for each Gaussian (state) in the model.

sample(n_samples=1, random_state=None)

Generate random samples from the model.

Parameters:

n_samples : int, optional

Number of samples to generate. Defaults to 1.

Returns:

X : array_like, shape (n_samples, n_features)

List of samples

score(X, y=None)

Compute the log probability under the model.

Parameters:

X : array_like, shape (n_samples, n_features)

List of n_features-dimensional data points. Each row corresponds to a single data point.

Returns:

logprob : array_like, shape (n_samples,)

Log probabilities of each data point in X

score_samples(X)

Return the likelihood of the data under the model.

Compute the bound on log probability of X under the model and return the posterior distribution (responsibilities) of each mixture component for each element of X.

This is done by computing the parameters for the mean-field of z for each observation.

Parameters:

X : array_like, shape (n_samples, n_features)

List of n_features-dimensional data points. Each row corresponds to a single data point.

Returns:

logprob : array_like, shape (n_samples,)

Log probabilities of each data point in X

responsibilities: array_like, shape (n_samples, n_components) :

Posterior probabilities of each mixture component for each observation

set_params(**params)

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as pipelines). The former have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Returns:self :

Examples using sklearn.mixture.DPGMM

Gaussian Mixture Model Ellipsoids

Gaussian Mixture Model Sine Curve