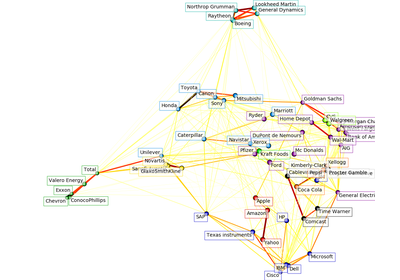
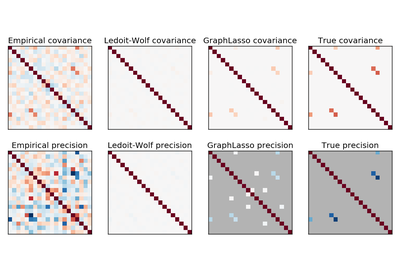
sklearn.covariance.GraphLassoCV¶
-
class
sklearn.covariance.GraphLassoCV(alphas=4, n_refinements=4, cv=None, tol=0.0001, enet_tol=0.0001, max_iter=100, mode='cd', n_jobs=1, verbose=False, assume_centered=False)[source]¶ Sparse inverse covariance w/ cross-validated choice of the l1 penalty
Read more in the User Guide.
Parameters: alphas : integer, or list positive float, optional
If an integer is given, it fixes the number of points on the grids of alpha to be used. If a list is given, it gives the grid to be used. See the notes in the class docstring for more details.
n_refinements: strictly positive integer :
The number of times the grid is refined. Not used if explicit values of alphas are passed.
cv : int, cross-validation generator or an iterable, optional
Determines the cross-validation splitting strategy. Possible inputs for cv are:
- None, to use the default 3-fold cross-validation,
- integer, to specify the number of folds.
- An object to be used as a cross-validation generator.
- An iterable yielding train/test splits.
For integer/None inputs
KFoldis used.Refer User Guide for the various cross-validation strategies that can be used here.
tol: positive float, optional :
The tolerance to declare convergence: if the dual gap goes below this value, iterations are stopped.
enet_tol : positive float, optional
The tolerance for the elastic net solver used to calculate the descent direction. This parameter controls the accuracy of the search direction for a given column update, not of the overall parameter estimate. Only used for mode=’cd’.
max_iter: integer, optional :
Maximum number of iterations.
mode: {‘cd’, ‘lars’} :
The Lasso solver to use: coordinate descent or LARS. Use LARS for very sparse underlying graphs, where number of features is greater than number of samples. Elsewhere prefer cd which is more numerically stable.
n_jobs: int, optional :
number of jobs to run in parallel (default 1).
verbose: boolean, optional :
If verbose is True, the objective function and duality gap are printed at each iteration.
assume_centered : Boolean
If True, data are not centered before computation. Useful when working with data whose mean is almost, but not exactly zero. If False, data are centered before computation.
Attributes: covariance_ : numpy.ndarray, shape (n_features, n_features)
Estimated covariance matrix.
precision_ : numpy.ndarray, shape (n_features, n_features)
Estimated precision matrix (inverse covariance).
alpha_ : float
Penalization parameter selected.
cv_alphas_ : list of float
All penalization parameters explored.
`grid_scores`: 2D numpy.ndarray (n_alphas, n_folds) :
Log-likelihood score on left-out data across folds.
n_iter_ : int
Number of iterations run for the optimal alpha.
See also
Notes
The search for the optimal penalization parameter (alpha) is done on an iteratively refined grid: first the cross-validated scores on a grid are computed, then a new refined grid is centered around the maximum, and so on.
One of the challenges which is faced here is that the solvers can fail to converge to a well-conditioned estimate. The corresponding values of alpha then come out as missing values, but the optimum may be close to these missing values.
Methods
error_norm(comp_cov[, norm, scaling, squared])Computes the Mean Squared Error between two covariance estimators. fit(X[, y])Fits the GraphLasso covariance model to X. get_params([deep])Get parameters for this estimator. get_precision()Getter for the precision matrix. mahalanobis(observations)Computes the squared Mahalanobis distances of given observations. score(X_test[, y])Computes the log-likelihood of a Gaussian data set with self.covariance_ as an estimator of its covariance matrix. set_params(**params)Set the parameters of this estimator. -
__init__(alphas=4, n_refinements=4, cv=None, tol=0.0001, enet_tol=0.0001, max_iter=100, mode='cd', n_jobs=1, verbose=False, assume_centered=False)[source]¶
-
error_norm(comp_cov, norm='frobenius', scaling=True, squared=True)[source]¶ Computes the Mean Squared Error between two covariance estimators. (In the sense of the Frobenius norm).
Parameters: comp_cov : array-like, shape = [n_features, n_features]
The covariance to compare with.
norm : str
The type of norm used to compute the error. Available error types: - ‘frobenius’ (default): sqrt(tr(A^t.A)) - ‘spectral’: sqrt(max(eigenvalues(A^t.A)) where A is the error
(comp_cov - self.covariance_).scaling : bool
If True (default), the squared error norm is divided by n_features. If False, the squared error norm is not rescaled.
squared : bool
Whether to compute the squared error norm or the error norm. If True (default), the squared error norm is returned. If False, the error norm is returned.
Returns: The Mean Squared Error (in the sense of the Frobenius norm) between :
`self` and `comp_cov` covariance estimators. :
-
fit(X, y=None)[source]¶ Fits the GraphLasso covariance model to X.
Parameters: X : ndarray, shape (n_samples, n_features)
Data from which to compute the covariance estimate
-
get_params(deep=True)[source]¶ Get parameters for this estimator.
Parameters: deep: boolean, optional :
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns: params : mapping of string to any
Parameter names mapped to their values.
-
get_precision()[source]¶ Getter for the precision matrix.
Returns: precision_ : array-like,
The precision matrix associated to the current covariance object.
-
mahalanobis(observations)[source]¶ Computes the squared Mahalanobis distances of given observations.
Parameters: observations : array-like, shape = [n_observations, n_features]
The observations, the Mahalanobis distances of the which we compute. Observations are assumed to be drawn from the same distribution than the data used in fit.
Returns: mahalanobis_distance : array, shape = [n_observations,]
Squared Mahalanobis distances of the observations.
-
score(X_test, y=None)[source]¶ Computes the log-likelihood of a Gaussian data set with self.covariance_ as an estimator of its covariance matrix.
Parameters: X_test : array-like, shape = [n_samples, n_features]
Test data of which we compute the likelihood, where n_samples is the number of samples and n_features is the number of features. X_test is assumed to be drawn from the same distribution than the data used in fit (including centering).
y : not used, present for API consistence purpose.
Returns: res : float
The likelihood of the data set with self.covariance_ as an estimator of its covariance matrix.
-
set_params(**params)[source]¶ Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as pipelines). The former have parameters of the form
<component>__<parameter>so that it’s possible to update each component of a nested object.Returns: self :