1.2. Linear and quadratic discriminant analysis¶

Linear discriminant analysis (lda.LDA) and quadratic discriminant analysis (qda.QDA) are two classic classifiers, with, as their names suggest, a linear and a quadratic decision surface, respectively.

These classifiers are attractive because they have closed-form solutions that can be easily computed, are inherently multiclass, and have proven to work well in practice. Also there are no parameters to tune for these algorithms.

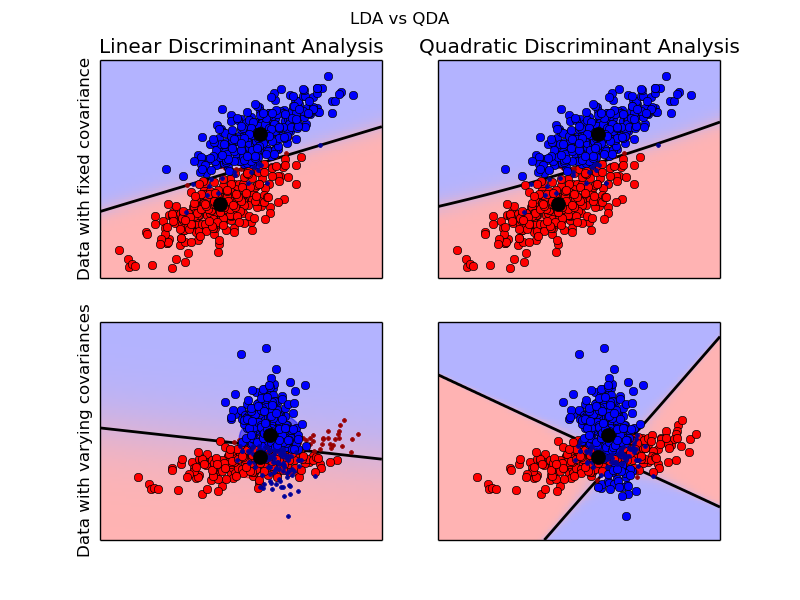
The plot shows decision boundaries for LDA and QDA. The bottom row demonstrates that LDA can only learn linear boundaries, while QDA can learn quadratic boundaries and is therefore more flexible.

Examples:

Linear and Quadratic Discriminant Analysis with confidence ellipsoid: Comparison of LDA and QDA on synthetic data.

1.2.1. Dimensionality reduction using LDA¶

lda.LDA can be used to perform supervised dimensionality reduction by projecting the input data to a subspace consisting of the most discriminant directions. This is implemented in lda.LDA.transform. The desired dimensionality can be set using the n_components constructor parameter. This parameter has no influence on lda.LDA.fit or lda.LDA.predict.

1.2.2. Mathematical Idea¶

Both methods work by modeling the class conditional distribution of the data 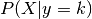$P(X|y=k)$ for each class 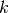$k$ . Predictions can be obtained by using Bayes’ rule:

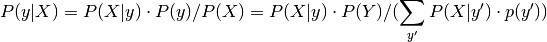
$P(y | X) = P(X | y) \cdot P(y) / P(X) = P(X | y) \cdot P(Y) / ( \sum_{y'} P(X | y') \cdot p(y'))$

In linear and quadratic discriminant analysis, 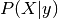$P(X|y)$ is modelled as a Gaussian distribution. In the case of LDA, the Gaussians for each class are assumed to share the same covariance matrix. This leads to a linear decision surface, as can be seen by comparing the the log-probability rations $log[P(y=k | X) / P(y=l | X)]$ .

In the case of QDA, there are no assumptions on the covariance matrices of the Gaussians, leading to a quadratic decision surface.

1.2.3. Shrinkage¶

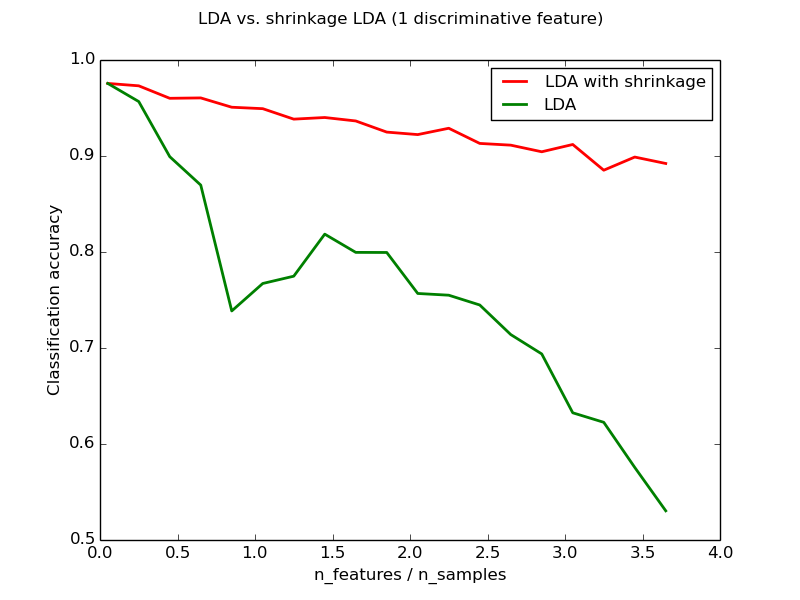
Shrinkage is a tool to improve estimation of covariance matrices in situations where the number of training samples is small compared to the number of features. In this scenario, the empirical sample covariance is a poor estimator. Shrinkage LDA can be used by setting the shrinkage parameter of the lda.LDA class to ‘auto’. This automatically determines the optimal shrinkage parameter in an analytic way following the lemma introduced by Ledoit and Wolf. Note that currently shrinkage only works when setting the solver parameter to ‘lsqr’ or ‘eigen’.

The shrinkage parameter can also be manually set between 0 and 1. In particular, a value of 0 corresponds to no shrinkage (which means the empirical covariance matrix will be used) and a value of 1 corresponds to complete shrinkage (which means that the diagonal matrix of variances will be used as an estimate for the covariance matrix). Setting this parameter to a value between these two extrema will estimate a shrunk version of the covariance matrix.

1.2.4. Estimation algorithms¶

The default solver is ‘svd’. It can perform both classification and transform, and it does not rely on the calculation of the covariance matrix. This can be an advantage in situations where the number of features is large. However, the ‘svd’ solver cannot be used with shrinkage.

The ‘lsqr’ solver is an efficient algorithm that only works for classification. It supports shrinkage.

The ‘eigen’ solver is based on the optimization of the between class scatter to within class scatter ratio. It can be used for both classification and transform, and it supports shrinkage. However, the ‘eigen’ solver needs to compute the covariance matrix, so it might not be suitable for situations with a high number of features.

Examples:

Normal and Shrinkage Linear Discriminant Analysis for classification: Comparison of LDA classifiers with and without shrinkage.

References:

Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning. Springer, 2009.

Ledoit O, Wolf M. Honey, I Shrunk the Sample Covariance Matrix. The Journal of Portfolio Management 30(4), 110-119, 2004.