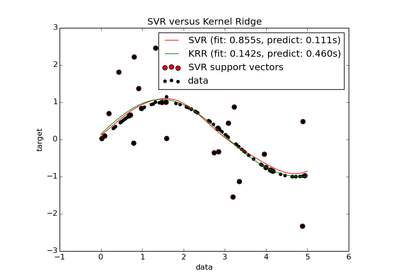
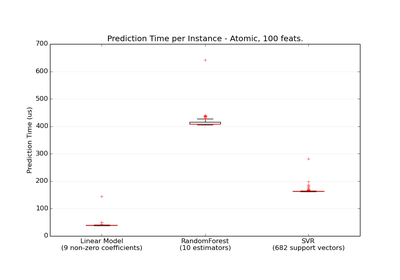
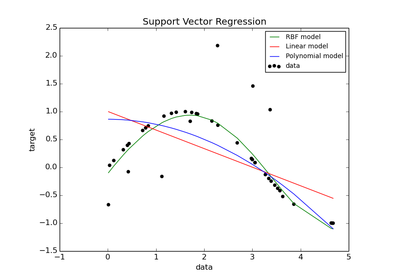
sklearn.svm.SVR

class sklearn.svm.SVR(kernel='rbf', degree=3, gamma=0.0, coef0=0.0, tol=0.001, C=1.0, epsilon=0.1, shrinking=True, cache_size=200, verbose=False, max_iter=-1)

Epsilon-Support Vector Regression.

The free parameters in the model are C and epsilon.

The implementation is based on libsvm.

Parameters:

C : float, optional (default=1.0)

Penalty parameter C of the error term.

epsilon : float, optional (default=0.1)

Epsilon in the epsilon-SVR model. It specifies the epsilon-tube within which no penalty is associated in the training loss function with points predicted within a distance epsilon from the actual value.

kernel : string, optional (default=’rbf’)

Specifies the kernel type to be used in the algorithm. It must be one of ‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’ or a callable. If none is given, ‘rbf’ will be used. If a callable is given it is used to precompute the kernel matrix.

degree : int, optional (default=3)

Degree of kernel function is significant only in poly, rbf, sigmoid.

gamma : float, optional (default=0.0)

Kernel coefficient for rbf and poly, if gamma is 0.0 then 1/n_features will be taken.

coef0 : float, optional (default=0.0)

independent term in kernel function. It is only significant in poly/sigmoid.

shrinking: boolean, optional (default=True) :

Whether to use the shrinking heuristic.

tol : float, optional (default=1e-3)

Tolerance for stopping criterion.

cache_size : float, optional

Specify the size of the kernel cache (in MB).

verbose : bool, default: False

Enable verbose output. Note that this setting takes advantage of a per-process runtime setting in libsvm that, if enabled, may not work properly in a multithreaded context.

max_iter : int, optional (default=-1)

Hard limit on iterations within solver, or -1 for no limit.

Attributes:

support_ : array-like, shape = [n_SV]

Indices of support vectors.

support_vectors_ : array-like, shape = [nSV, n_features]

Support vectors.

dual_coef_ : array, shape = [1, n_SV]

Coefficients of the support vector in the decision function.

coef_ : array, shape = [1, n_features]

Weights assigned to the features (coefficients in the primal problem). This is only available in the case of linear kernel.

coef_ is readonly property derived from dual_coef_ and support_vectors_.

intercept_ : array, shape = [1]

Constants in decision function.

See also

NuSVR

Support Vector Machine for regression implemented using libsvm using a parameter to control the number of support vectors.

LinearSVR

Scalable Linear Support Vector Machine for regression implemented using liblinear.

Examples

>>> from sklearn.svm import SVR
>>> import numpy as np
>>> n_samples, n_features = 10, 5
>>> np.random.seed(0)
>>> y = np.random.randn(n_samples)
>>> X = np.random.randn(n_samples, n_features)
>>> clf = SVR(C=1.0, epsilon=0.2)
>>> clf.fit(X, y) 
SVR(C=1.0, cache_size=200, coef0=0.0, degree=3, epsilon=0.2, gamma=0.0,
    kernel='rbf', max_iter=-1, shrinking=True, tol=0.001, verbose=False)

Methods

decision_function(X)	Distance of the samples X to the separating hyperplane.
fit(X, y[, sample_weight])	Fit the SVM model according to the given training data.
get_params([deep])	Get parameters for this estimator.
predict(X)	Perform regression on samples in X.
score(X, y[, sample_weight])	Returns the coefficient of determination R^2 of the prediction.
set_params(**params)	Set the parameters of this estimator.

__init__(kernel='rbf', degree=3, gamma=0.0, coef0=0.0, tol=0.001, C=1.0, epsilon=0.1, shrinking=True, cache_size=200, verbose=False, max_iter=-1)

decision_function(X)

Distance of the samples X to the separating hyperplane.

Parameters:

X : array-like, shape = [n_samples, n_features]

For kernel=”precomputed”, the expected shape of X is [n_samples_test, n_samples_train].

Returns:

X : array-like, shape = [n_samples, n_class * (n_class-1) / 2]

Returns the decision function of the sample for each class in the model.

fit(X, y, sample_weight=None)

Fit the SVM model according to the given training data.

Parameters:

X : {array-like, sparse matrix}, shape (n_samples, n_features)

Training vectors, where n_samples is the number of samples and n_features is the number of features. For kernel=”precomputed”, the expected shape of X is (n_samples, n_samples).

y : array-like, shape (n_samples,)

Target values (class labels in classification, real numbers in regression)

sample_weight : array-like, shape (n_samples,)

Per-sample weights. Rescale C per sample. Higher weights force the classifier to put more emphasis on these points.

Returns:

self : object

Returns self.

Notes

If X and y are not C-ordered and contiguous arrays of np.float64 and X is not a scipy.sparse.csr_matrix, X and/or y may be copied.

If X is a dense array, then the other methods will not support sparse matrices as input.

get_params(deep=True)

Get parameters for this estimator.

Parameters:

deep: boolean, optional :

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

params : mapping of string to any

Parameter names mapped to their values.

predict(X)

Perform regression on samples in X.

For an one-class model, +1 or -1 is returned.

Parameters:

X : {array-like, sparse matrix}, shape (n_samples, n_features)

For kernel=”precomputed”, the expected shape of X is (n_samples_test, n_samples_train).

Returns:

y_pred : array, shape (n_samples,)

score(X, y, sample_weight=None)

Returns the coefficient of determination R^2 of the prediction.

The coefficient R^2 is defined as (1 - u/v), where u is the regression sum of squares ((y_true - y_pred) ** 2).sum() and v is the residual sum of squares ((y_true - y_true.mean()) ** 2).sum(). Best possible score is 1.0, lower values are worse.

Parameters:

X : array-like, shape = (n_samples, n_features)

Test samples.

y : array-like, shape = (n_samples) or (n_samples, n_outputs)

True values for X.

sample_weight : array-like, shape = [n_samples], optional

Sample weights.

Returns:

score : float

R^2 of self.predict(X) wrt. y.

set_params(**params)

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as pipelines). The former have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Returns:self :

Examples using sklearn.svm.SVR

Comparison of kernel ridge regression and SVR

Prediction Latency

Support Vector Regression (SVR) using linear and non-linear kernels