Note
Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder
Comparison of Manifold Learning methods¶
An illustration of dimensionality reduction on the S-curve dataset with various manifold learning methods.
For a discussion and comparison of these algorithms, see the manifold module page
For a similar example, where the methods are applied to a sphere dataset, see Manifold Learning methods on a severed sphere
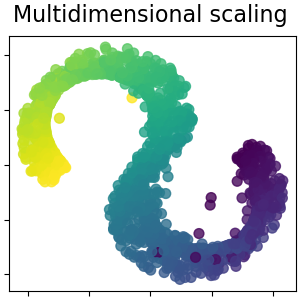
Note that the purpose of the MDS is to find a low-dimensional representation of the data (here 2D) in which the distances respect well the distances in the original high-dimensional space, unlike other manifold-learning algorithms, it does not seeks an isotropic representation of the data in the low-dimensional space.
# Author: Jake Vanderplas -- <vanderplas@astro.washington.edu>
Dataset preparation¶
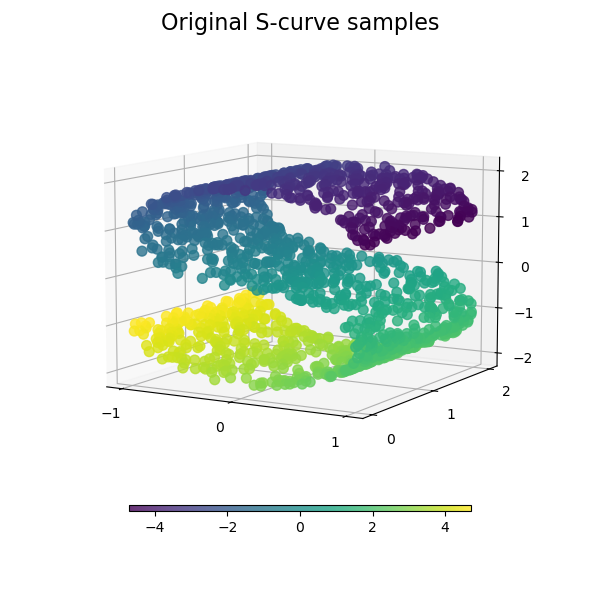
We start by generating the S-curve dataset.
import matplotlib.pyplot as plt
# unused but required import for doing 3d projections with matplotlib < 3.2
import mpl_toolkits.mplot3d # noqa: F401
from matplotlib import ticker
from sklearn import datasets, manifold
n_samples = 1500
S_points, S_color = datasets.make_s_curve(n_samples, random_state=0)
Let’s look at the original data. Also define some helping functions, which we will use further on.
def plot_3d(points, points_color, title):
x, y, z = points.T
fig, ax = plt.subplots(
figsize=(6, 6),
facecolor="white",
tight_layout=True,
subplot_kw={"projection": "3d"},
)
fig.suptitle(title, size=16)
col = ax.scatter(x, y, z, c=points_color, s=50, alpha=0.8)
ax.view_init(azim=-60, elev=9)
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
ax.yaxis.set_major_locator(ticker.MultipleLocator(1))
ax.zaxis.set_major_locator(ticker.MultipleLocator(1))
fig.colorbar(col, ax=ax, orientation="horizontal", shrink=0.6, aspect=60, pad=0.01)
plt.show()
def plot_2d(points, points_color, title):
fig, ax = plt.subplots(figsize=(3, 3), facecolor="white", constrained_layout=True)
fig.suptitle(title, size=16)
add_2d_scatter(ax, points, points_color)
plt.show()
def add_2d_scatter(ax, points, points_color, title=None):
x, y = points.T
ax.scatter(x, y, c=points_color, s=50, alpha=0.8)
ax.set_title(title)
ax.xaxis.set_major_formatter(ticker.NullFormatter())
ax.yaxis.set_major_formatter(ticker.NullFormatter())
plot_3d(S_points, S_color, "Original S-curve samples")
Define algorithms for the manifold learning¶
Manifold learning is an approach to non-linear dimensionality reduction. Algorithms for this task are based on the idea that the dimensionality of many data sets is only artificially high.
Read more in the User Guide.
n_neighbors = 12 # neighborhood which is used to recover the locally linear structure
n_components = 2 # number of coordinates for the manifold
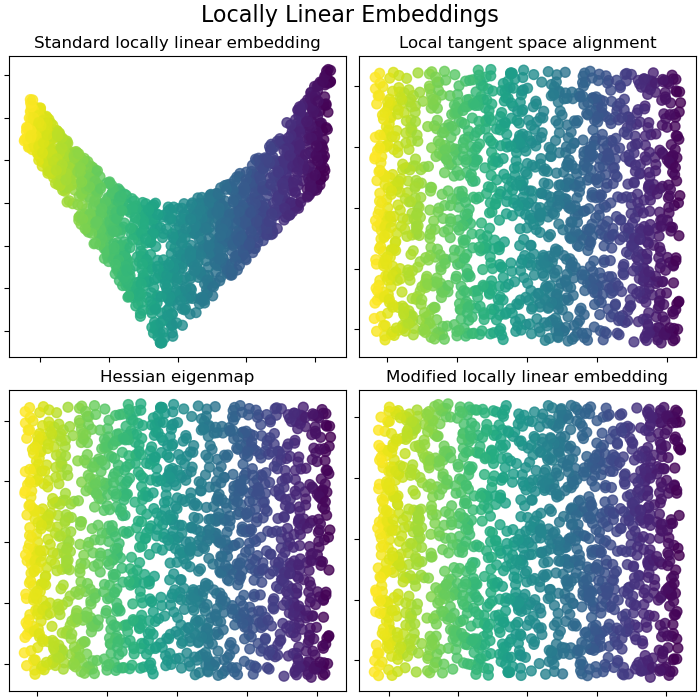
Locally Linear Embeddings¶
Locally linear embedding (LLE) can be thought of as a series of local Principal Component Analyses which are globally compared to find the best non-linear embedding. Read more in the User Guide.
params = {
"n_neighbors": n_neighbors,
"n_components": n_components,
"eigen_solver": "auto",
"random_state": 0,
}
lle_standard = manifold.LocallyLinearEmbedding(method="standard", **params)
S_standard = lle_standard.fit_transform(S_points)
lle_ltsa = manifold.LocallyLinearEmbedding(method="ltsa", **params)
S_ltsa = lle_ltsa.fit_transform(S_points)
lle_hessian = manifold.LocallyLinearEmbedding(method="hessian", **params)
S_hessian = lle_hessian.fit_transform(S_points)
lle_mod = manifold.LocallyLinearEmbedding(method="modified", **params)
S_mod = lle_mod.fit_transform(S_points)
fig, axs = plt.subplots(
nrows=2, ncols=2, figsize=(7, 7), facecolor="white", constrained_layout=True
)
fig.suptitle("Locally Linear Embeddings", size=16)
lle_methods = [
("Standard locally linear embedding", S_standard),
("Local tangent space alignment", S_ltsa),
("Hessian eigenmap", S_hessian),
("Modified locally linear embedding", S_mod),
]
for ax, method in zip(axs.flat, lle_methods):
name, points = method
add_2d_scatter(ax, points, S_color, name)
plt.show()
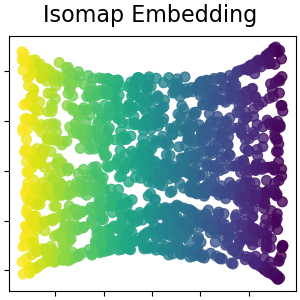
Isomap Embedding¶
Non-linear dimensionality reduction through Isometric Mapping. Isomap seeks a lower-dimensional embedding which maintains geodesic distances between all points. Read more in the User Guide.
isomap = manifold.Isomap(n_neighbors=n_neighbors, n_components=n_components, p=1)
S_isomap = isomap.fit_transform(S_points)
plot_2d(S_isomap, S_color, "Isomap Embedding")
Multidimensional scaling¶
Multidimensional scaling (MDS) seeks a low-dimensional representation of the data in which the distances respect well the distances in the original high-dimensional space. Read more in the User Guide.
md_scaling = manifold.MDS(
n_components=n_components,
max_iter=50,
n_init=4,
random_state=0,
normalized_stress=False,
)
S_scaling = md_scaling.fit_transform(S_points)
plot_2d(S_scaling, S_color, "Multidimensional scaling")
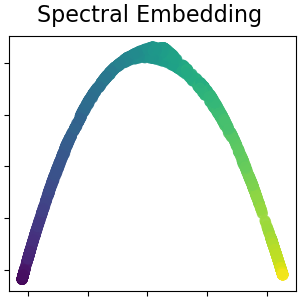
Spectral embedding for non-linear dimensionality reduction¶
This implementation uses Laplacian Eigenmaps, which finds a low dimensional representation of the data using a spectral decomposition of the graph Laplacian. Read more in the User Guide.
spectral = manifold.SpectralEmbedding(
n_components=n_components, n_neighbors=n_neighbors, random_state=42
)
S_spectral = spectral.fit_transform(S_points)
plot_2d(S_spectral, S_color, "Spectral Embedding")
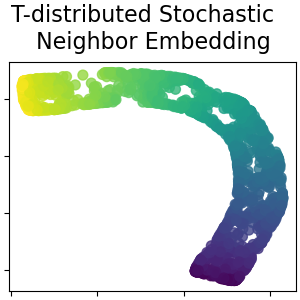
T-distributed Stochastic Neighbor Embedding¶
It converts similarities between data points to joint probabilities and tries to minimize the Kullback-Leibler divergence between the joint probabilities of the low-dimensional embedding and the high-dimensional data. t-SNE has a cost function that is not convex, i.e. with different initializations we can get different results. Read more in the User Guide.
t_sne = manifold.TSNE(
n_components=n_components,
perplexity=30,
init="random",
max_iter=250,
random_state=0,
)
S_t_sne = t_sne.fit_transform(S_points)
plot_2d(S_t_sne, S_color, "T-distributed Stochastic \n Neighbor Embedding")
Total running time of the script: (0 minutes 11.901 seconds)
Related examples

Manifold learning on handwritten digits: Locally Linear Embedding, Isomap…
t-SNE: The effect of various perplexity values on the shape